
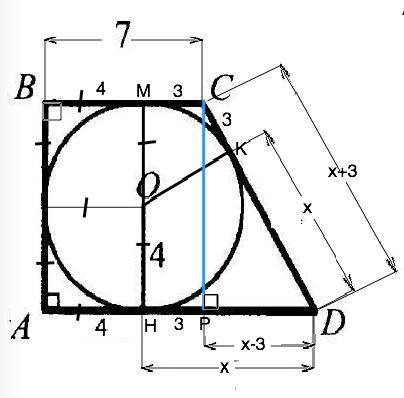
Вариант решения.
В прямоугольной трапеции АВСD радиус вписанной окружности 4, длина меньшего основания 7. Найдите площадь трапеции.
Высота трапеции равна диаметру вписанной окружности. АВ⊥АD ⇒ AB=h=2r=8.
Проведем радиусы ОМ к ВС и ОК к CD. Радиусы, проведенные в точку касания, перпендикулярны касательной. АВМН - прямоугольник. ВМ=АН=4. МС=7-4=3.
Отрезки касательных, проведенные из точки вне окружности, равны. СК=СМ=3 и НD=KD=х. Опустим высоту СР=AB=8. Отрезок НР=МС=3, PD=х-3, СD=х+3.
По т.Пифагора СD²-PD²=CP². (х+3)²-(х-3)² =64, откуда 12х=64 и х=5 1/3. Площадь трапеции равна произведению высоты на полусумму оснований. АD=AH+HD=4+5 1/3=9 ¹/₃. S(ABCD)=AB•(BC+AD):2=8•(7+9 ¹/₃):2. Ѕ(ABCD)=65 ¹/₃ ед. площади.
Проведённая к плоскости перпендикулярная прямая пересекает плоскость в точке О. На прямой отложен отрезок АD), точка О является серединной точкой этого отрезка. Определи вид и периметр Δ АВD, если АD = 11 см, а ОВ = 5 см (ответ округли до одной десятой).
Объяснение:
1) ΔАОВ=ΔDOB как прямоугольные (ВО⊥AD) по двум катетам :ВО=DО=5,5 ,BO-общий ⇒ AB=DB ⇒Δ АВD равнобедренный .
2)Найдем боковые стороны из ΔАОВ-прямоугольного по т. Пифагора АВ=√(5,5²+5²)=√55,25≈5,43≈5,4 .