Смотри разбор
Объяснение:
1) Пусть в параллелограмме ABCD, ∠A = 65°.
∠C = ∠A = 65° ⇒ ∠C = 65°.
Параллелограмм это выпуклый четырёхугольник, поэтому сумма его углов равна 360°.
∠A + ∠B + ∠C + ∠D = 360°; 2·65° + 2·∠B = 360° |:2 ; ∠B = 180° - 65° = 115°.
∠D = ∠B = 115° ⇒ ∠D = 115°.
ответ: 65°, 115° и 115°.
2 ) Противоположные стороны параллелограмма равны по его определению, значит вторая меньшая сторона тоже равна 11 см. Значит большая сторона будет равна (54-22):2=16 см.
3) Сумма углов трапеции равна 360 градусов. В трапеции два угла прямоугольные (равны 90 градусов), а один равен 20 градусов - по условию. Отсюда неизвестный угол равен 360-90-90-20 = 160 градусов
ответ: 90°, 90° и 160°
1) Периметр трапеции равен АВ+ВС+СД+АД, тогда АВ+ВД=64-24-30=10
АВ=ВД=5 см., т.к. трапеция равнобедренная.
2) Проведем высоты ВН и СМ, тогда четырехугольник ВНМС будет параллелограммом, т.к. ВН || СМ (высоты), ВС || НМ (как основания)
ВС=НМ, ВН=СМ по св-ву параллелограмма.
3) НМ=24, тогда АН+МД=30-24=6, а АН=МД, т.к. прямоугольные треугольники равны (док-во из первой задачи)
АН=МД=3 см.
По теореме пифагора найдем ВН=4
4) Площадь трапеции равна половине произведения оснований, помноженное на высоту, т.е. 24+30/2 * 4=108 см.2
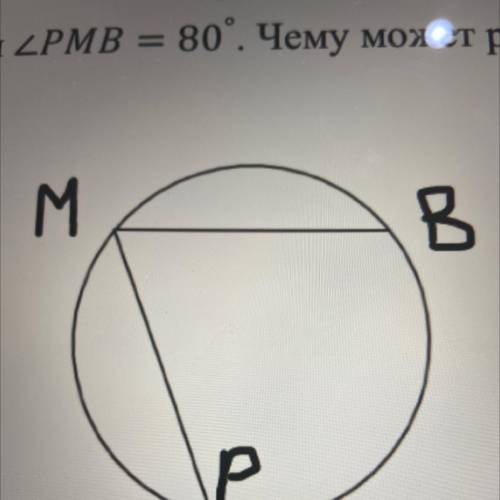
160 т.к. дуга больше вписанного угла в два раза