5,2 см и 9,6 см²
Объяснение:
Расстояния - это перпендикуляры. Проводя из точки пересечения диагоналей перпендикуляры к сторонам, получаем, что половина диагонали, заключенная между этими перпендикулярами, является диагональю в маленьком(зеленом) прямоугольнике, образованном ими, т.е. по т. Пифагора она равна √(1²+2,4²)=2,6 см. Вся диагональ в два раза больше, т.е. она равна 5,2 см.
Большой прямоугольник в свою очередь можно разбить на 4 маленьких, образованных перпендикулярами, проведенными из точки пересечения диагоналей. Т.е. его площадь в четыре раза больше, чем площадь одного маленького. Площадь маленького равна 1×2,4=2,4 см², тогда площадь исходного прямоугольника равна 2,4×4=9,6 см²
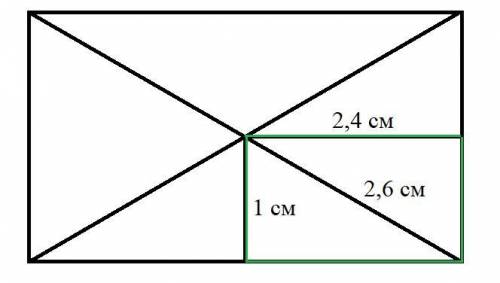
5,2 см и 9,6 см²
Объяснение:
Расстояния - это перпендикуляры. Проводя из точки пересечения диагоналей перпендикуляры к сторонам, получаем, что половина диагонали, заключенная между этими перпендикулярами, является диагональю в маленьком(зеленом) прямоугольнике, образованном ими, т.е. по т. Пифагора она равна √(1²+2,4²)=2,6 см. Вся диагональ в два раза больше, т.е. она равна 5,2 см.
Большой прямоугольник в свою очередь можно разбить на 4 маленьких, образованных перпендикулярами, проведенными из точки пересечения диагоналей. Т.е. его площадь в четыре раза больше, чем площадь одного маленького. Площадь маленького равна 1×2,4=2,4 см², тогда площадь исходного прямоугольника равна 2,4×4=9,6 см²

По теореме о высоте, проведенной из вершины прямого угла в прямоугольном треугольнике имеем:
BC^2=BD*AB,
ab=BC^2/BD=36/3=12
ответ. АВ=12 см.