Доказательство:
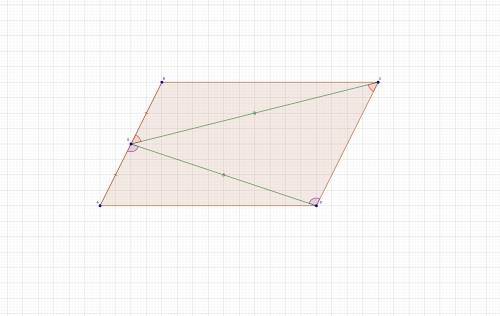
Т.к. ABCD - параллелограмм, то AB//CD и AD//BC.
∠ECD = ∠CEB как накрест лежащие при параллельных прямых AB и CD и секущей EC.
∠EDC = ∠DEA как накрест лежащие при параллельных прямых AB и CD и секущей ED.
Т.к. EC = ED , то ΔECD - равнобедренный с основанием CD.
Значит ∠ECD = ∠EDC как углы при основании.
Следовательно ∠CEB = ∠DEA
ΔEBC = ΔEAD по двум сторонам и углу между ними (EB = EA по условию.)
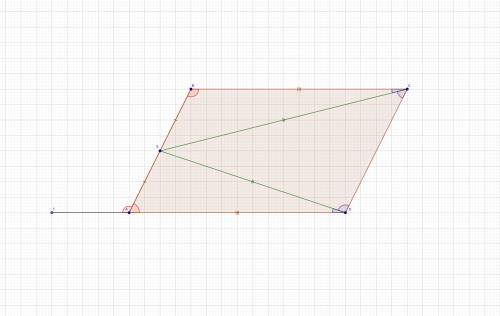
См. рисунок 2.
Из равенства треугольников EBC и EAD следует, что ∠EBC = ∠EAD
и ∠BCE = ∠ADE
∠BCD = ∠BCE + ∠ECD
∠ADC = ∠ADE + ∠EDC
Следовательно ∠BCD = ∠ADC
Продолжим сторону AD влево.
∠FAB = ∠ABC как накрест лежащие при параллельных прямых AD и BC и секущей AB.
∠FAB = ∠ADC как соответственные при параллельных прямых AB и DC и секущей AD
Собирая все вместе получаем, что ∠ABC = ∠BCD = ∠CDA = ∠DAB
Получается, что ABCD - параллелограмм в котором все углы равны. Следовательно ABCD - прямоугольник
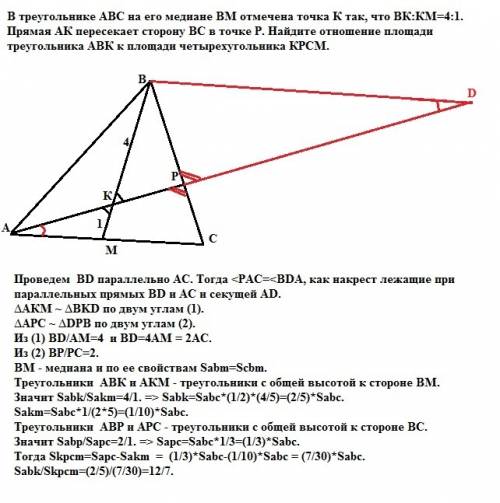
сначала нарисуй горизонтальную линию. Выбери любую точку F. восставь из нее вверх перепендикуляр к исходной прямой. На горизонтальной линии от точки F циркулем отложи вправо два одинаковых отрезка любой длины потом установи радиус циркуля равный длине двух отрезков и установив острие циркуля в правый конец первого отрезка В, сделай засечку на вертикальном перпендикуляре. Получишь точку С. Угол FСВ равен З0 градусам, потому что ВС - гипотенуза прямоугольного треугольника АВС, которая в два раза больше его катета АВ. Раздели угол АСВ циркулем и линейкой пополам, то есть построй его биссектрису СД Получишь угол АСД 15 градусов затем из точки С восставь к прямой АС перпендикляр влево поставь на нем любую точку H Угол HСД равен 105 градусов.