свойства углов параллелограмма: противоположные углы равны, а прилежащие к одной стороне в сумме составляют 180°.
Если в задании примеры на нахождение углов, прилежащих к одной стороне, то можем решать с уравнений.
1) один угол равен 52°, три остальных 52°-это ему противолежащий, и два угла по 180°-52°=128°.
2) речь о противоположных углах, в сумме 174°, значит, каждый по 174°/2=87°, тогда два других по 180°-87°=93°
3)один угол х, второй х+28, в сумме 180, значит, х+х+28=180⇒х+14=90;
х=90-14=76, значит, два угла по 76°, а два других по 76°+28°=104°
4) меньший угол х, больший 4х, уравнение х+4х=180; х=180/5=36
Два угла по 36°, два других по 4*36°=144°
5)один угол 4х, второй 5х, здесь х>0, это коэффициент пропорциональности, 4х+5х=180;х=180/9=20, значит, один угол 20°*4=80°, ему противоположный тоже 80°, а два других 180°-80°=100°, или 20°*5=100°
Окружность с центром О.
ВС - диаметр.
А ∈ окружности с центром О.
∠АОС = 35°
Найти:∠ВАО - ?
Решение:
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
⇒ ∠ВАО + ∠ОВА = 35° (∠АОС = 35°, по условию)
Так как ∠ОВА = ∠ВАО, по свойству ⇒ ∠ОВА = ∠ВАО = 35°/2 = 17,5°
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Сумма смежных углов равна 180°.
∠АОС смежный с ∠ВОА ⇒ ∠ВОА = 180° - 35° = 145°
Сумма углов треугольника равна 180°.
⇒ ∠ВАО = ∠ОВА = (180° - 145°)/2 = 17,5°
ответ: 17,5°.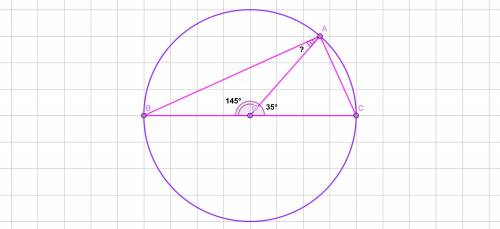
V=4*4*6=16*6=96
ответ: V=96 см³