ABC - прямоугольный треугольник (∠A = 90)
AB = 18; AK = KH = 8 (KH⊥BC)
BH = √(BK² - KH²) = √((18 - 8)² - 8²) = 6
cos(∠B) = BH/BK = 6/10
BC = AB/cos(∠B) = 30
или рассмотреть подобные треугольники KBH и CBA
AC = √(BC² - AB²) = 24
P = 24 + 18 + 30 = 72 (см)
50, а проекция наклонной равна 6 см. Чему равна длина перпендикуляра, проведённого из этой же точки к плоскости?
4) Если прямая перпендикулярна двум радиусам круга, как она расположена по отношению к самому кругу?
5) Сколько можно провести прямых перпендикулярных данной прямой через данную точку, если а) эта точка лежит на прямой; б) эта точка не лежит на прямой?
6) Как между собой располагаются две прямые перпендикулярные одной и той же плоскости?
7) Могут ли перпендикуляр и наклонная, проведённые из одной и той же точки, иметь равные длины?
Тема: "окружающая среда"
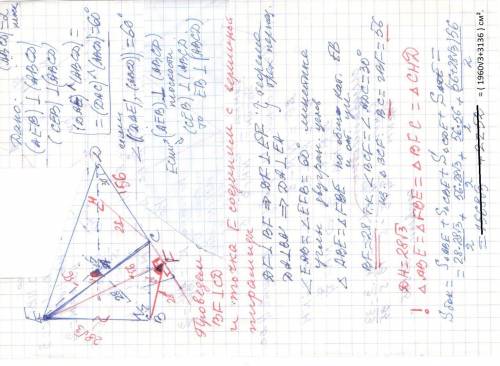
* * * для удобства плоскость (ABCD) обозначаем через Ψ * * *
EABCD - пирамида , основание которой трапеция ABCD ;
AD || BC ; AB =28 ; ∠A =∠B =90° ; ∠D =30° ; | [AB] < [CD] ; [BC] < [AD]
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ; ∠ ( (CDE) , Ψ ) =∠ ( (ADE) , Ψ ) = 60°
--------------------------
1. Трапеция ABCD ПРЯМОУГОЛЬНАЯ
- - -
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ⇒ EB ⊥ Ψ
DA⊥ BA ⇒DA ⊥ EA ; ∠EAB =60° линейный угол двугранного угла
EADC ; Построим линейный угол двугранного угла EDCA
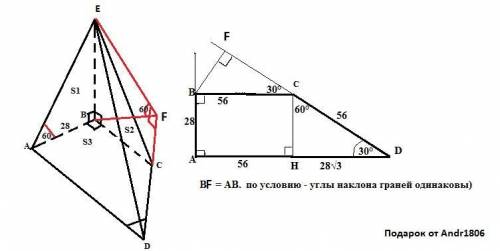
Проведем BF ⊥ CD и основание F этого перпендикуляра соединим с вершиной ПИРАМИДЫ E. Получаем ∠EFB = 60° линейный угол двугранного угла EDCA .
* * * ! ΔABE = ΔFBE =Δ BFC = ΔCHD учитывая ∠D =∠BCF =30° * * *
Вычисление площадей боковых граней и т.д. cм приложение
Тр. ВОМ подобен тр АВС (угол ВОМ = 90 град.( МО - расстояние), угол В - общий , Угол ВМО = углу ВСА (это выходит из равенства предыдущих углов))
Найдем ВО по т. Пифагора из прямоугольного тр. МВО
BO^2 = BM^2 - MO^2
BO^2= 36
BO = 6 см
Коэффициент подобия этих треугольников к = ВА/ ВО = 18/6=3( коэффициент подобия треугольников равен отношению сходственных сторон)
Периметр МВО = ВМ+ВО+МО= 24 см
Периметр АВС = Периметр МВО* к = 24*3 = 72 см(Отношение периметров подобных треугольников равно коэффициенту подобия)
ответ: 72 см