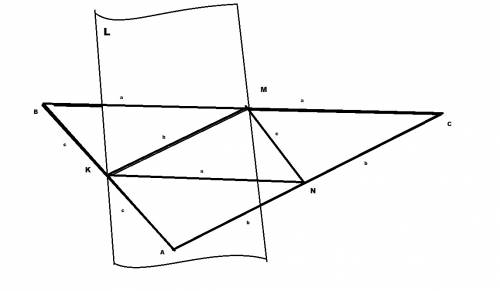
(отрезанный четырехугольник - трапеция)
LL1 - линия пересечения плоскости L и треуг.ABC, LL1 проходит через середину AB и || AC => LL1 - средняя линия треугольника ABC, LL1 = 1/2 * AC или AC = 2LL1
отрезанный плоскостью маленький треугольник BLL1 подобен треуг.ABC BB1 : ABC = 1 : 2
высота треуг.BLL1 (h) относится к высоте треуг.ABC (H) h : H = 1 : 2, т.е. H = 2h
S(BLL1) = 1/2 * LL1 * h
S(ABC) = 1/2 * AC * H = 1/2 * 2LL1 * 2h = 4 * S(BLL1)
S(BLL1) = 1/4 * S(ABC)
Sтрапеции = = S(ABC) - S(BLL1) = S(ABC) - 1/4*S(ABC) = 3/4 * S(ABC)
S(ABC) = 4/3 * Sтрапеции = 4/3 * 24 = 4*8 = 32
1. В основании – прямоугольник, поэтому треугольник ABD – прямоугольный. По теореме Пифагора находится его гипотенуза.
BD−→−=AB2+AD2−−−−−−−−−−√=62+82−−−−−−√=10
2. Достроим четырехугольник KPRM, где P и R – середины BB1 и DD1 соответственно.
По признаку параллелограмма все четыре получившихся четырехугольника ABPK,BCMP,CMRD и AKRD – параллелограммы.
Следовательно, KPRM – тоже параллелограмм, причем равный основаниям параллелепипеда. А значит, и прямоугольник.
Диагонали прямоугольника KM=PR=BD= равны. Следовательно, KM−→−=10
3. Рассмотрим прямоугольный треугольник CC1L. Угол CC1L равен углу B1BC, который в свою очередь равен 60° по условию. Следовательно, угол C1CL=30°. По теореме о катете напротив угла в 30° гипотенуза CC1=2⋅LC1=2⋅4=8.
И CC1−→−=8
4. Рассмотрим треугольник B1CC1.
Его уголCC1B1=60° , его стороны CC1 и B1C1
Объяснение:
ні не існує я спитав в вчительки вона сказала ні