S = 10,08 ед.изм2
или
S = 10 8/100 ед.изм2 (десять целых восемь сотых единиц измерения в квадрате)
Объяснение:
1). Данную трапецию разделим на 3 сегмента:
1 Прямоугольник и 2 боковых треугольника.
2). Найдем площади данных фигур: (в клетках)
а). Sпр = 6 * 7 = 42 кл2.
б). Sтр1 = 5 * 6 / 2 = 15 кл2.
в). Sтр2 = 2 * 6 / 2 = 6 кл2.
Сумма данных сегментов будет являться площадью трапеции (в клетках):
г). Sтр = 42 + 15 + 6 = 63 кл2.
Единицы измерения не указаны, возможно см2, но продолжим так, зная размер клетки, получим площадь в ед.изм.:
S = 0,4 * 0,4 * 63 = 0,16 * 63 = 10,08 ед.изм2.
или
S = 4/10 * 4/10 * 63 = (4 * 4)/(10 * 10) * 63 = 16/100 * 63 = (16 * 63)/(100 * 1) = 1008/100 = 10 8/100 ед.изм2 (десять целых восемь сотых единиц измерения в квадрате)
60 ед²
Объяснение:
Пусть прямоугольный треугольник АВС. Угол С=90°. Точка касания делит гипотенузу на отрезки: х и 17-х. Отрезки катетов от вершин А и В до точек касания равны х и 17-х, как касательные, проведенные из одной точки. Отрезки катетов от вершины С до точек касания равны радиусу вписанной окружности, то есть равны 3. Тогда катеты равны х+3 и 17-х+3 = 20-х. По Пифагору:
(х+3)² + (20-х)² = 17² => x² - 17х +60 =0. =>
х1=5, х2 =12. => катеты равны 8 и 15 ед. в обоих случаях.
Sabc = (1/2)*8*12 = 60 ед².
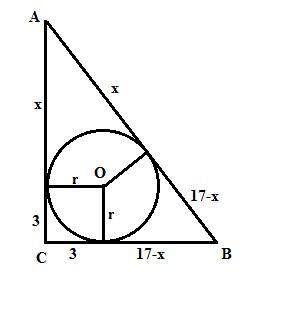
рисунок D
Объяснение:
это рисунок D, потому что сумма двух данных углов равна 180 градусам