
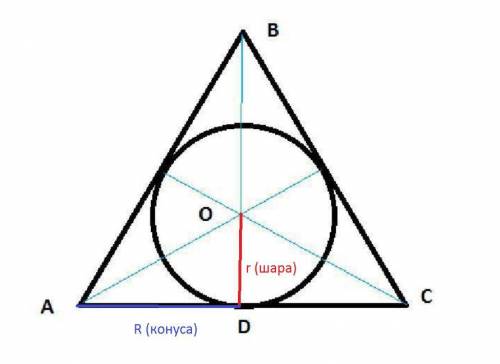
Осевое сечение конуса – равнобедренный треугольник АВС.
АВ=ВС – образующие.
BD– высота конуса, а также высота, медиана и биссектриса равнобедренного треугольника.
О–центр вписанной в треугольник АВС окружности и центр вписанного в конус шара.
ОD=r .
AD=R .
Из прямоугольного треугольника
tg∠OAD = tg(α/2) = r/R . Отсюда r = Rtg(α/2).
ОА– биссектриса угла ВAD, так как центр вписанной в треугольник окружности– точка пересечения биссектрис.
Высота конуса H = R/tg(α/2).
V(шара) = (4/3)πr³ = (4/3)πR³tg³(α/2).
V(конуса)=(1/3)S(осн)·H=(1/3)·πR²·R/tg(α/2) = (1/3)·πR³/tg(α/2).
Разделим V(конуса) на V(шара).
V(конуса) / V(шара) = ( (1/3)·πR³/tg(α/2)) / ((4/3)πR³tg³(α/2)) = 4tg³(α/2)tgα.
ответ: V(конуса) = V(шара) / (4tg³(α/2)tgα).
а). Чтобы найти координаты точки, симметричной точке А(-3;1), надо провести прямую через эту точку и начало координат. Затем от начала координат отложить на этой прямой отрезок, равный отрезку от точки А до начала координат. Конец отложенного отрезка и даст нам координаты искомой точки В(3;-1). Это ответ.
б). Чтобы найти координаты точки, симметричной точке А(-3;1) относительно оси абсцисс (оси Х), надо провести прямую через точку А перпендикулярно оси Х и отложить на этой прямой отрезок равный расстоянию от точки А до оси Х (координаты Ya). Таким образом искомая точка имеет координаты
С(-3;-1). Это ответ.
1)BD-общая
2)<CDB=<ADB-условие
3)<CBD=<ABD-AD биссиктрисса
Это 2 признак.
Т. К треугольники равны, соответственно стороны тоже ровны