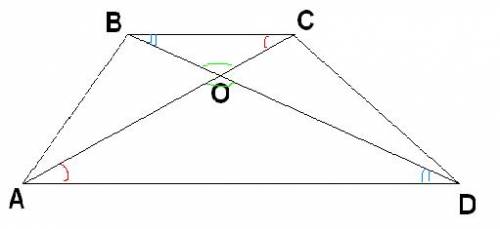
По определению трапеции её основания параллельны: BC||AD .
Рассмотрим треугольники BOC и DOA:
1) Угол BCO равен углу OAD ( как накрест лежащие при пересечении параллельных прямых BC и AD секущей AC )
2) Угол CBO равен углу ODA ( как накрест лежащие при пересечении параллельных прямых BC и AD секущей BD )
Следовательно, треугольники BOC и DOA подобны.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
k (коэф. подобия) равен отношению сходственных сторон подобных треугольников =>
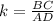
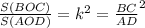
Вторая задача: Прямая ВС лежит в плоскости (АВС), так как 2 её точки В и С лежат в плоскости (АВС). Прямая АМ пересекает плоскость (АВС) в точке А, не лежащей на ВС, значит АМ и ВС скрещивающиеся прямые.
Третья задача: PK средняя линия треугольника АВС, поэтому равна 1/2 ВС=8:2=4Доказательство. МН средняя линия треугольника DBC (по условию), значит МН || BC и с плоскостью МНК. не имеет общих точек, поэтому РК тоже не может иметь с ВС общих точек, но РК и ВС лежат в одной плоскости треугольника АВС, значит РК и ВС параллельны. Так, как к середина АС, то и Р должна быть серединой АВ.
Этого хватит, ты мало выставил, так бы все решил. Удачи!!