Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Можно решить задачу уравнением с одним неизвестным.
Пусть один из отрезков первой хорды будет х, а другой 24-х
Тогда 10*8=х(24-х)
Получим квадратное уравнение
х²-24х+80=0
D=b²-4ac=-24²-4·1·80=256
Так как дискриминант больше нуля, то уравнение имеет два корня
х₁ =20
х₂ =4
Отрезки первой хорды будут иметь длину 20 см и 4 см
Здесь главное сделать правильный чертеж, остальное уже просто.
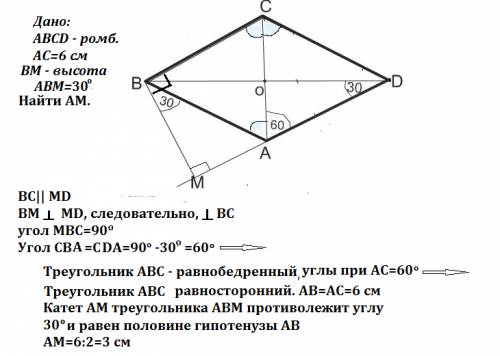
Так как высота проведена к продолжению АD, она находится вне ромба.
ВМ - высота, перпендикулярна МD.
ВС и АD параллельны как стороны параллелограмма, ⇒
ВМ перпендикулярна ВС, угол МВС=90º
Угол МВА=30ª, тогда угол СВА=90º-30º=60º. Т.к. стороны ромба равны, треугольник АВС - равнобедренный. Углы при основании АС=(180º-60º):2=60º⇒
ΔАВС - равносторонний.
Тогда АВ=АС=6 см.
В прямоугольном треугольнике АМВ углу МВА противолежит катет МА.
Катет, противолежащий углу 30º, равен половине гипотенузы.
АМ=АВ:2=3 см
Строй окружность, все сделай так как на рисунке, а теперь решение:
Есть у хорд окружности такое свойство:при пересечении двух хорд окружности получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.
То есть, AE*BE=DE*CE
DE*CE=10*8=80
DE+CE=24
Система уравнений у нас получается, решаем, заменив DЕ - x, а СЕ - у
ответ:20 и 4 см