Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.
Центр шара, вписанного в правильную пирамиду, лежит на её высоте.
Формула радиуса вписанной окружности для тетраэдра
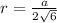
По этой формуле 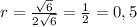
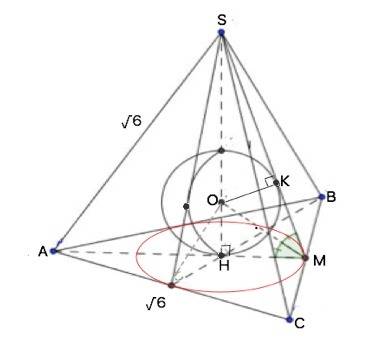
Подробное решение.(см. рисунок вложения)
Обозначим пирамиду SABC, SH - высота пирамиды, SM - апофема.
ОН и ОК - радиусы вписанного шара,
Проведем сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды. При этом сечение шара будет вписанной в угол SМA окружностью.
∆ SHM прямоугольный. НМ - радиус окружности, вписанной в основание АВС пирамиды.
НМ=АМ:3 ( радиус вписанной в правильный треугольник окружности),
Так как тетраэдр правильный и, все его грани - правильные треугольники, их апофемы равны высоте правильного треугольника со стороной √6.
SM=AM=√6•√3/2=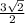
Радиус НМ вписанной в основание окружности равен AM/3=√2/2
КM=НM=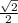
SK=SM-KM=3√2/2-√2/2=√2
∆SHM подобен ∆SKO ⇒
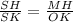 ⇒
⇒
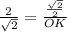 ⇒
⇒
4r=2
r=0,5
650 см²
Объяснение:
Дано: КМРТ - трапеция, МК⊥КТ, МК=20 см, РТ=25 см. МТ - биссектриса. Найти S(КМРТ).
∠КТМ=∠РТМ по определению биссектрисы
∠РМТ=∠МТК как внутренние накрест лежащие при МР║КТ и секущей МТ, значит ΔМРТ - равнобедренный, МР=РТ=25 см.
Проведем высоту РН=МК=20 см.
КН=МР=25 см.
ΔРТН - прямоугольный, РТ=25 см, РН=20 см, значит ТН=15 см (египетский треугольник).
КТ=КН+ТН=25+15=40 см.
S=(МР+КТ):2*РН=(25+40):2*20=650 см²