a = 5, b = 12
Вычислим диагональ основания параллелепипеда:
d = √(a² + b²) = √(25 +144) = √(169) = 13
Наклон в 45° диагонали D параллелепипеда к основанию означает, что диагональ основания d и высота параллелепипеда H одинаковые
H = d = 13.
Периметр основания Р = 2a + 2b = 10 + 24 = 34
Площадь основания Sосн = a·b = 5·12 = 60
Площадь поверхности параллелепипеда
S = 2Sосн +Р·Н = 2·60 + 34·13 = 562(см²)
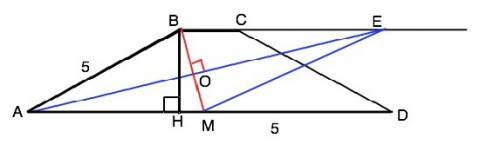
Опустим из вершины В высоту трапеции ВН. Высота равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности, а больший - полусумме оснований. АН=(10-2):2=4 см Из треугольника АВН по т. Пифагора ВН=3 см.
Противоположные стороны трапеции параллельны. Биссектриса угла ВАD при них – секущая. ∠ВЕА=∠ЕАD – накрестлежащие. Но ∠ВАЕ=∠ЕАD, т.к. АЕ - биссектриса. ⇒ ∆ АВЕ - равнобедренный (т.к.углы при основании АЕ равны). АВ=ВЕ=5 см.
Проведем из Е параллельно АВ прямую до пересечения с АD в точке М. В параллелограмме АВЕМ противоположные стороны параллельны и равны, значит, ЕМ=АВ=ВЕ=АМ=5, ⇒ АВЕМ - ромб.
Высота трапеции ВН - высота ромба. Площадь ромба равна произведению высоты на сторону, к которой проведена. Ѕ(АВЕМ)=ВН•АМ=3•5=15 см²
Биссектриса угла АВЕ – меньшая диагональ ромба ВМ и образует с высотой ромба и частью его стороны прямоугольный треугольник ВНМ, в котором ВН и МН - катеты. ВН=3 см, МН=АМ-АН=1см По т.Пифагора ВМ=√(BH²+HM²)=√(9+1)=√10. Биссектриса ВО угла АВЕ в ∆ АВЕ равна половине ВМ. ВО=(√10)/2; BO²=10/4=2,5 см²
Опустим из вершины В высоту трапеции ВН. Высота равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности, а больший - полусумме оснований. АН=(10-2):2=4 см Из треугольника АВН по т. Пифагора ВН=3 см.
Противоположные стороны трапеции параллельны. Биссектриса угла ВАD при них – секущая. ∠ВЕА=∠ЕАD – накрестлежащие. Но ∠ВАЕ=∠ЕАD, т.к. АЕ - биссектриса. ⇒ ∆ АВЕ - равнобедренный (т.к.углы при основании АЕ равны). АВ=ВЕ=5 см.
Проведем из Е параллельно АВ прямую до пересечения с АD в точке М. В параллелограмме АВЕМ противоположные стороны параллельны и равны, значит, ЕМ=АВ=ВЕ=АМ=5, ⇒ АВЕМ - ромб.
Высота трапеции ВН - высота ромба. Площадь ромба равна произведению высоты на сторону, к которой проведена. Ѕ(АВЕМ)=ВН•АМ=3•5=15 см²
Биссектриса угла АВЕ – меньшая диагональ ромба ВМ и образует с высотой ромба и частью его стороны прямоугольный треугольник ВНМ, в котором ВН и МН - катеты. ВН=3 см, МН=АМ-АН=1см По т.Пифагора ВМ=√(BH²+HM²)=√(9+1)=√10. Биссектриса ВО угла АВЕ в ∆ АВЕ равна половине ВМ. ВО=(√10)/2; BO²=10/4=2,5 см²

Диагональ основания 13, поэтому высота параллелепипеда 13, площадь поверхности 2*(5*12 + 5*13 + 12*13) = 562
Немного поясню :))) диагональ основания делит прямоугольник в основании на 2 Пифагоровых треугольника с катетми 5 и 12, отсюда и берется 13.
Вместе с диагональю параллелепипеда и боковым ребром диагональ основания образует прямоугольный треугольник с острым углоам 45 градусов, поэтому боковое ребро равно диагонали основания.