№1.
R - радиус описанной окружности, r - радиус окружности, вписанной в квадрат, а - сторона правильного шестиугольника, х - сторона квадрата, S - площадь круга.
R=a=20
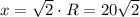
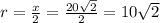
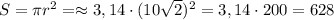
ответ: площадь круга, вписанного в квадрат, 628.
№2.
а - сторона правильного шестиугольника
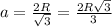
ответ: сторона правильного шестиугольника 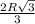 .
.
№3.
Каждый из пяти углов правильного пятиугольника равен
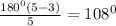 .
.
Если провести две диагонали из одного угла, то они разделят пятиугольник на три треугольника. Рассмотрим два треугольника, в которых две из сторон являются сторонами исходного пятиугольника. Эти треугольники равны по первому признаку равенства треугольников, кроме того, они оба равнобедренные. Величина равных углов равна  . Угол между диагоналями будет равен
. Угол между диагоналями будет равен 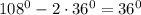
ответ: угол между двумя диагоналями, проведенными из одной вершины правильного пятиугольника, равен 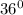 .
.
Объяснение:
Чтобы найти расстояние от точки В до касательной окружности, мы можем использовать свойство перпендикулярности касательной и радиуса окружности, проведенного в точке касания.
Обозначим точку касания касательной и окружности как точку P.
Обозначим центр окружности как точку O.
Обозначим точку В как точку B.
По условию, диаметр окружности AB равен 24 см, что означает, что радиус окружности равен половине диаметра, то есть 12 см.
Также известно, что расстояние от точки A до касательной (проведенной в точке P) равно 4 см.
Согласно свойству касательной и радиуса, радиус, проведенный в точке касания, будет перпендикулярен касательной. Это означает, что треугольник AOP является прямоугольным, где OA - радиус окружности, OP - расстояние от точки A до касательной.
Теперь мы можем использовать теорему Пифагора для нахождения длины отрезка OP:
OP^2 + OA^2 = AP^2
4^2 + 12^2 = AP^2
16 + 144 = AP^2
160 = AP^2
AP = √160 = 4√10
Таким образом, расстояние от точки B до касательной будет равно расстоянию от точки A до касательной:
BP = AP = 4√10
Итак, расстояние от точки В до касательной равно 4√10 см.