По одной из формул: площадь треугольника равна половине произведения длин его сторон на синус угла между ними.
При пересечении диагоналей вертикальные углы равны.
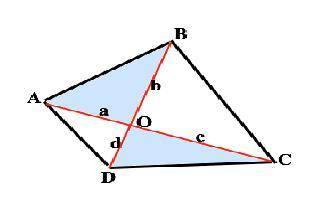
Пусть ∠АОВ=∠DOC=α Тогда смежные им ∠DOA=∠BOC=180°- α. sinα=sin(180°- α)
Примем АО=а, ВО=b, СО=с, DO=d. Тогда:
S(AOB)=a•b•sinα/2
Ѕ(DOC)=d•c•sinα/2
S(AOB)•Ѕ(DOC)=a•b•c•d•sin²α/4
S(AOD)=a•d•sinα/2
S(BOC)=b•c•sinα /2
S(AOD)•S(BOC)=a•d•b•c•sin²α/4
a•b•c•d•sin²α/4 =a•d•b•c•sin²α/4 ⇒
S(AOB)•Ѕ(DOC)= S(AOD)•S(BOC), что и требовалось доказать.
4)
Так как треугольник равнобедренный, то углы при основании — равны.
И так как каждый из них равен 62°, то угол, противолежащий основанию — равен: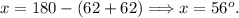
//Надо заметить, что сумма внутренних углов треугольника — всегда равна 180°.//
5)
Чтобы треугольник существовал, сумма каждых двух сторон — должна быть больше каждой оставшийся стороны, тоесть:
Проверим: 7.2+4.3 = 11.5.
Третья сторона не должна быть равна, или больше чила 11.5, тоесть длина оставшийся стороны может максимально равна: 11.499999.
6)
//Нет рисунка//
7) Один из углов треугольника три раза меньше второго и на 150 больше третий. Найдите углы треугольника.
Объявим этот же угол — как переменная "x".
Второй угол, который больше "x" в 3 раза — будет объявлен как: "3x";
Третий угол, который меньше "x" на 150° — будет объявлен как" "x-150".
Составим уравнение:
Как мы видим — один из углов больше суммы всех углов треугольника, а другой-то вообще — отрицательный.
Я опробовала много вариантов, спобом подборки, всё равно не получилось найти целые — соответствующие углам треугольника числа.
Или задача с ошибков, или вот — правильный ответ: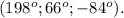
8) Внешний угол равен 105°, что и означает, что внутренний и смежной с ним углов равен: 180-105 = 75°.
По теореме внешнего угла: сумма двух оставшихся внутренних углов, не смежных со внешним углом — равен этому же внешнему углу.
Тоесть сумма двух оставшихся углов равна: x+y = 105°.
Так как их отношения равно — 4:3, то переменные таковы: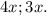
Составим уравнение: