Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
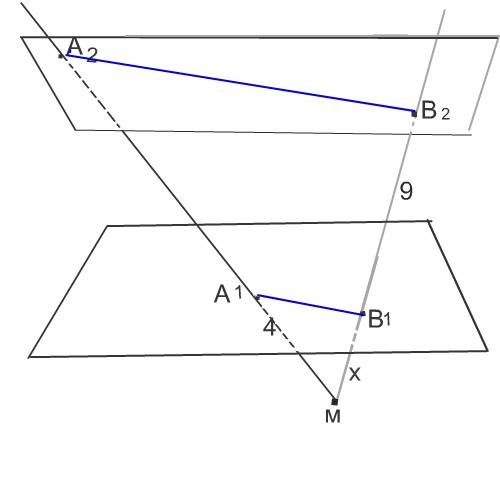
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольники МА2В2 и МА1В1 подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольникиМА2В2 и МА1В1подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
Так как дана правильная призма, то в основании лежит равносторонний треугольник, а боковые грани - прямоугольники. Боковой кант равен высоте призмы. Рассматривая боковую грань, с теоремы Пифагора находишь боковой кант. Далее применяешь формулы. S(боковое)=P(переметр основания)*h. S(полное)=S(боковое)+2S(основания). И так как в основе равносторонний треугольник, то его S=(сторона умножить на корень из 3)/4. Вот краткое решение.