Рассмотрим прямоугольный треугольник АВС, где угол А прямой. Вписанная окружность касается катета АВ в точке М, где АМ=2, МВ=8. Точка касания окружности со стороной АС точка Р, центр окружности точка О. Линии проведенные к точкам касания из цетра вписанной окружности перпендикулярны сторонам и являютс радиусами. Тогда тогда АМОР является квадратом и стороны равны 2. АМ=АР как касательные к окружности, проведенные из одной точки. Рассмотрим треугольник ВМО. у него угол М прямой, МВ и МО являются катетами. Отношение МО к МВ равно тангенсу угла МВО (tg альфа).Значит тангенс МВО=2/8=1/4. Так как центр вписанной окружности лежит на пересечением биссектрис, то ВО является биссектрисой угла АВС и равен 2МВО. Найдем тагенс АВС по формуле двойного угла. он равен 2tg альфа деленное на
1-tg^2 альфа. Подставив значения получаем 8/15. A в треугольнике АВС катет АВ=2+8=10, tg АВС=8/15, найдем катет АС=АВ*tgАВС=10*8/15=80/15=16/3=5 1/3, а гипотенузу находим по теореме Пифагора.ВС^2=10^2+(16/3)^2=1156/9
ВС=34/3=11 1/3 Получаем АВ=10, АС=5 1/3, а ВС=11 1/3
1)Рассмотрим парал-м АBCD.
Угол В =150 ,значит угол А = (360-2*150):2 =30
2)S парал-ма = Высота на основание ( а * h)
Пусть основание равно 16( а=16), то боковая сторона равна 12.
Есть правило ! Катет, лежащий, против угла в 30 градусов равен половине гипотенузы ! Значит , катет ,который лежит против угла в 30градусов в нашем случаи равен 12 :2 =6. 6-это высота для парал-ма.
Вернёмся в формулу площади парал-ма : S = а * h.
Подставим
S ABCD =16 *6 = 96 см^2
НЕ ЗАБЫВАЕМ , ЧТО ПЛОЩАДЬ ИЗМЕРЯЕТСЯ В САНТИМЕТРАХ КВАДРАТНЫХ !
ответ : S ABCD = 96 см^2
Объяснение:
Дано:
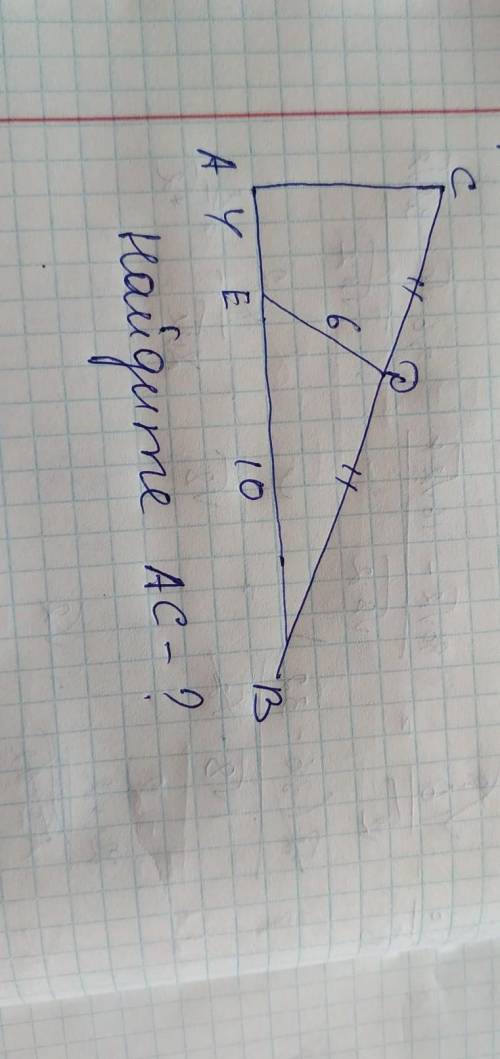
ΔABC - прямоугольный (∠A = 90°)
AB = 14
AE = 4
EB = 10
ED = 6
(•) D - середина гипотенузы (BC)
Найти:
AC
• Пусть половина гипотенузы (BC) = x, т.е.:
CD = DB = x
• Рассмотрим ΔEDB, по теореме косинусов:
ED² = EB² + DB² - 2 • EB • DB • cos∠CBD
( cos∠CBD = AB/CB = 14/2x )
6² = 10² + x² - 2 • 10 • x • 14/2x
36 = 100 + x² - 20x • 14/2x
36 = 100 + x² - 140
x² - 76 = 0
x² = 76
x = √76
x = √(4 • 19)
x = 2√19
• Находим гипотенузу:
BC = 2 • x = 2 • 2√19 = 4√19
• В прямоугольном треугольнике ABC по теореме Пифагора:
BC² = AB² + AC², ⇒ AC = √(BC² - AB²)
AC = √((4√19)² - 14²) = √(304 - 196) = √108 = 6√3
ответ: AC = 6√3