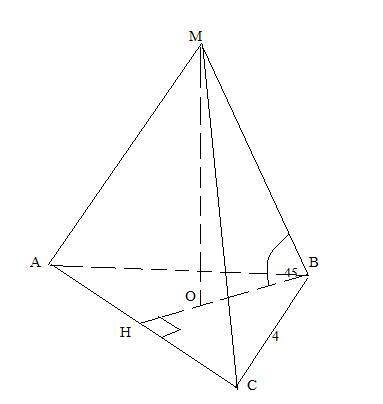
Основанием правильной пирамиды служит равносторонний треугольник со стороной 4 см. Каждое боковое ребро пирамиды составляет с плоскостью основания угол 45º.
Найти площадь полной поверхности пирамиды.
Объяснение:
1)S(полн.пир)=S(осн)+S(бок)
S(осн)=S( прав.тр)=(а²√3)/4 , где а-сторона основания,
S(бок)=1/2 Р(осн)*d , где d-апофема.
2) Высота пирамиды МО , в правильной пирамиде, проецируется в центр основания, точку пересечения медиан . Пусть ВН⊥АС.
В ΔАВС: a₃=R√3 , 4=R√3 , R=4/√3 (см) ⇒ r=ОН=2/√3 (см) по т. о точке пересечения медиан.
Т.к по условию ∠МВО=45°, то ΔМВО-прямоугольный , равнобедренный. Значит ВО=МО=4/√3 см.
ΔМОН-прямоугольный, по т. Пифагора МН=√( ОН²+ОМ²),
МН=√( (2/√3)²+(4/√3)²)=2√(5/3) (см) ⇒ d=2√(5/3) см.
3) S(бок)=1/2*2√(5/3) *12= 12√(5/3) (см²) .
S(осн)=(4²√3)/4=4√3 ( см²)
S(полн.пир)=4√3 +12√(5/3)=4√3 +4√15 (см²)
ответ. 102.
Объяснение:
Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10