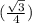Дан куб ABCDA1B1C1D1. Точка O - центр грани AA1BB1. Найдите угол между прямыми DO и CD1. Решите задачу с метода координат. (Если можно, то сделайте , с рисунком)
DO и CD₁ - скрещиваются, но А₁В ║ CD₁ ⇒ угол между прямыми DO и CD₁ равен углу между прямыми DO и А₁В. Пусть ребро исходного куба равно единице: АВ = 1, тогда диагональ грани равна корню из двух: А₁В = √2. Рассмотрим ΔDАO – прямоугольный (DА ⊥ АO), по теореме Пифагора: DO² = АO² + DА², АО = 0,5*АВ₁ = ⇒
DO² = .
Далее рассмотрим ΔDOВ, где ∠DOВ = углу между прямыми DO и А₁В =
= углу между прямыми DO и CD₁. При этом DВ = √2 как диагональ квадрата с единичной стороной, ОВ = , DO² = .
По теореме косинусов: DВ² = DO² + ОВ² – 2 · DO · ОВ · сos(∠DOВ) ⇒
Биссектриса разделяет прямоугольный треугольник на два треугольника. Под углом 80 градусов означает, что угол, совместный с данным по развернутой гипотенузе равен 180-80=100. Больший угол прямоугольного треугольник - 90 градусов. значит углы, на которые разделила биссектриса равны 90/2=45. значит у нас известны по два угла каждого треугольника . Из этого мы можем вычислить остальные два угла, которые и являются неизвестными углами прямоугольного треугольника. 180-80-45=55 градусов и 180-100-45=35 градусов
Пусть ad = a1d1 — равные биссектрисы, ∠a = ∠a1, ac = a1c1 — равные стороны. в δаdс = δa1d1c1: ∠dac = ∠d1a1c1 (т.к. ∠dac половина угла ∠bac ∠dac = ∠bac : 2 = ∠b1a1c1 : 2 = ∠d1a1c1). ad = a1d1, ас = а1с1. (по условию: ad = a1d1 — равные биссектрисы, aс = a1c1 — равные прилежащие стороны). таким образом, δadc = δа1d1c1 по 1-му признаку равенства треугольников, откуда ∠с = ∠с1 как лежащие против равных сторон в равных треугольниках) в δabcи δа1в1с1: ас = а1с1, ∠а = ∠а1 (по условию) ∠с = ∠с1. таким образом, δabc = δа1в1с1 по 1-му признаку равенства треугольников, что и требовалось доказать.
DO и CD₁ - скрещиваются, но А₁В ║ CD₁ ⇒ угол между прямыми DO и CD₁ равен углу между прямыми DO и А₁В. Пусть ребро исходного куба равно единице: АВ = 1, тогда диагональ грани равна корню из двух: А₁В = √2. Рассмотрим ΔDАO – прямоугольный (DА ⊥ АO), по теореме Пифагора: DO² = АO² + DА², АО = 0,5*АВ₁ =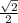 ⇒
⇒
DO² =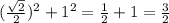 .
.
Далее рассмотрим ΔDOВ, где ∠DOВ = углу между прямыми DO и А₁В =
= углу между прямыми DO и CD₁. При этом DВ = √2 как диагональ квадрата с единичной стороной, ОВ =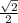 , DO² =
, DO² = 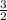 .
.
По теореме косинусов: DВ² = DO² + ОВ² – 2 · DO · ОВ · сos(∠DOВ) ⇒
√2² =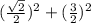
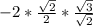 * сos(∠DOВ) ⇒
* сos(∠DOВ) ⇒
√3*сos(∠DOВ) =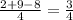 ⇒ сos(∠DOВ) =
⇒ сos(∠DOВ) = 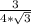 =
= 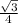 ⇒
⇒
∠DOВ = углу между прямыми DO и CD₁ = arccos