1)Треугольники подобны ⇒ и у другого треугольника стороныотносятся как 3х/4х/5х. Большая сторона - 5х, и она равна 15.
15=5х
х=3
тогда первая сторона 3х=9, вторая 4х=12
Периметр равен:9+12+15=36
ответ:36
2)Больший катет лежит против большего отрезка гипотенузы. По свойству катет в прямоугольном треугольнике есть среднее геометрическое между гипотенузой (16+9=25см) и его проекцией на гипотенузу (16см)
х=√(25*16)=20см
ответ:20см
3)Рисунок внизу.
В ΔABD по теореме косинусов:
cosABC=(AB²+BD²-AD²)/(2AB*BD)=(16+1-12,25)/(2*4*1)=4,75/8
В ΔABC по теореме косинусов:
AC²=AB²+BC²-2*AB*BC*cosABC=16+256-2*4*16*4,75/8=196
AC=14
ответ:14
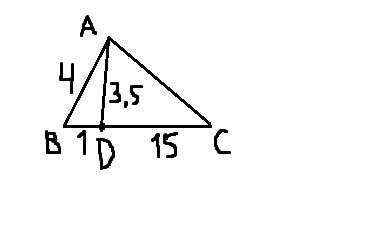
R=3/cos 18=3/0.95=3.15 (см).
Найдем сторону фигуры:
a=2*3.15*sin 180/n=2*3.15*0.3=1.89 (см)
ответ: 1.89 см.
2) Найдем R:
R = r/cos 180/n=5/√3/2=10√3/3 (см)
Длина стороны равна R, следовательно a=R=10√3/3, значит,
P = 6a=10√3/3*6=20√3 (cм) или 34.64 см.
ответ: 20√3 см или 34.64 см.
3) Радиус описанной около 6-угольника окружности = длине стороны, следовательно R = 5√3 см. Для треугольника эта же окружность является вписанной, т.е. для треугольника r=5√3. В свою очередь, R=2r=2*5√3=10√3 (см). Сторону правильного треугольника можно вычислить по формуле a=R√3=10√3*√3=10*3=30 (см).
ответ: 30 см.