Объяснение:
1. Це клясичний трикутник Піфагора.
Прямий кут між катетами 3 та 4, тобто площа рахується як площа будь-якого прямокутного трикутника: 0.5*3*4=6
2. АВС - також трикутник Піфагора з кутами А=60, B=30, C=90 катетом 3 гіпотенузою 5, а отже іншим катетом 4. Отже площа АВС, рахується як в попередньому завдан і дорівнює 6
3. Уявімо ромб як 2 рівних і тимчасово рівнобедрених трикутника зі стороною a, та із звгальною підставою b, яка є діагоналлю рмба. Площа такого трикутника рахується за формулую:
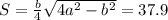
Оскільки трикутників 2 - то S ромба = 37.9*2=75.8
Объяснение:
1. Це клясичний трикутник Піфагора.
Прямий кут між катетами 3 та 4, тобто площа рахується як площа будь-якого прямокутного трикутника: 0.5*3*4=6
2. АВС - також трикутник Піфагора з кутами А=60, B=30, C=90 катетом 3 гіпотенузою 5, а отже іншим катетом 4. Отже площа АВС, рахується як в попередньому завдан і дорівнює 6
3. Уявімо ромб як 2 рівних і тимчасово рівнобедрених трикутника зі стороною a, та із звгальною підставою b, яка є діагоналлю рмба. Площа такого трикутника рахується за формулую:
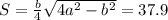
Оскільки трикутників 2 - то S ромба = 37.9*2=75.8
Окружность с центром в точке А( 5 ; 6 ) . Диаметр ВС , В( 3 ; 4 ) ,
С ( 7 ; 8 ) .
б) Построим ΔВСD , как показано на рисунке . ∠D=90° ,
∠CBD=∠BCD=45° ⇒ k = tg∠CBD = tg45° = 1 .
Если продлить прямую ВС , то она пересечёт ось ОУ в точке с ординатой, равной b=1 .
Получим уравнение прямой в виде y = kx + b такое : у = х+1 .
а) Из ΔBCD по теореме Пифагора найдём ВС .
ВС²=ВD²+CD²=4^2+4^2=16+16=32 , BC=√32 = 4√2
ВC - диаметр окружности ⇒ радиус равен половине диаметра ⇒
R=2√2=√8 .
Уравнение окружности имеет вид (x-5)² + (y-6)² = 8 .