Дано: АВС-прямоугольный треугольник
ВК=КС, т.к. АК-медиана
угол А=90 град.
ВС=60см
1.Если это прямоугольный треугольник, то допустим угол при вершине В=30град, а в следствии при вершине С=60град, при этом раскладе углов катет АС, лежащий напротив угла в 30град= половине гипотенузы, т.е =30см.
2. Медиана по своим свойства делитгипотенузу пополам, т.е. ВК=КС=30см.
3. Рассмотрим образовавшийся треугольник АКС, у него: КС=30см, АС=30см, значит треугольник АКС- равнобедренный, а угол С=60град, далее...
т.к. АКС - равнобедренный треугольник угол КАС=углу АКС=(180-уголС):2=(180-60):2=60град. Значит треуг АКС равносторонний, т.к все углы у него равны, отсюда АК=КС=АС=30см
ответ:АК=30см.
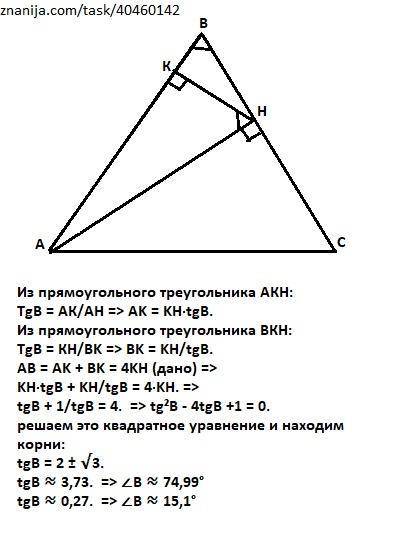
1. ∠АBС ≈ 75° .
2. ∠АBС ≈ 15° .
Объяснение:
Треугольник АВН - прямоугольный (AH — высота равнобедренного треугольника ABC - дано). НК - высота из прямого угла. =>
Треугольники АВН, АКН и ВКН подобные. => ∠ ABC = ∠АНК.
Из прямоугольного треугольника АКН:
TgB = АК/АН => AK = KH·tgB.
Из прямоугольного треугольника BКН:
TgB = КH/BK => BK = KH/tgB.
AB = AK + BK = 4KH (дано) =>
KH·tgB + KH/tgB = 4·KH. =>
tgB + 1/tgB = 4. => tg²B - 4tgB +1 = 0.
Решаем это квадратное уравнение и находим корни:
tgB = 2 ± √3.
tgB ≈ 3,73. => ∠B ≈ 74,99° ≈ 75° .
tgB ≈ 0,27. => ∠B ≈ 15,1° ≈ 15° .
v = 72 км/ч = 20 м/с
радиус R = v^2/a = 20^2/4 =100 м