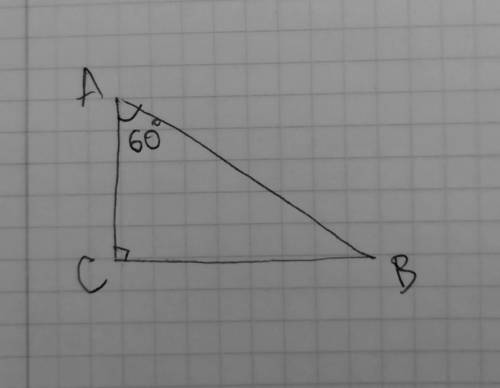
в прямоугольном треугольнике ABC угол C = 90°, угол A = 60°, так? если да, то
по свойству углов треугольника,
угол B = 180° – 90° – 60° = 30°
катет, лежащий против угла в 30°, равен половине гипотенузы. Это и есть меньший катет. Получается
AC = AB / 2, AB = 2 * AC [1]
по условию задания, AB + AC = 36.9 см [2]
подставим [1] в [2], получим
2 * AC + AC = 36.9
3 * AC = 36.9
AC = 36.9 / 3 = 12.3 см
подставим полученное значение в [1], получим
AB = 2 * AC = 2 * 12.3 = 24.6 см
Итого, гипотенуза равна 24.6 см, меньший катет равен 12.3 см
l=2
l=2*9*
Длина дуги находится по формуле:
2) l=2
l=
2
r=
Найдем a:
Далее вспомним формулу радиуса описанной окружности около правильного треугольника:
Подставив a, найдем R.
И, наконец, найдем длину окружности, описанную около этого треугольника: