1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
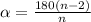
Найдем при каком n угол будет равен 160°:
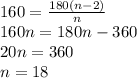
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
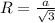
Подставим заданное значение стороны:
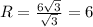
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
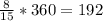 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см
Глубины вод измерялись раньше лотом, то есть веревкой с привязанным грузом. Сейчас измеряют используя отраженный звуковой или ультразвуковой сигнал. Скорость известна, время измеряется, глубина вычисляется. Для измерения небольших (метров, сантиметров, миллиметров) расстояний используются рулетки, метры, аршины, линейки, в общем приборы со шкалой, градуированной в единицах длины. Сейчас все чаще используются лазерные дальномеры, работающие на принципе измерения расстояния до Луны. Правда эти приборы сразу показывают расстояние. Строители до сих пор активно используют разные теодолиты. Масштабные измерения земной поверхности уже давно проводят с аэрофотосъемок или съемок из космоса. Маленькие размеры (меньше миллиметра измеряют с разного рода микрометров. Совсем маленькие, межатомные, вычисляются используя сложные технологии, но тоже измеряются.
Вообще, измерение расстояний - одно из базовых измерений, на которых покоится познание мира и приборы для этого все время улучшаются, придумывают новые.