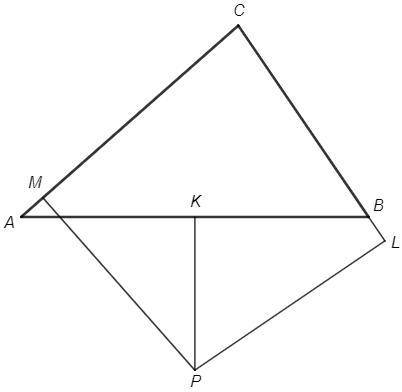
Пусть P - произвольная точка
PK, PL, PM - перпендикуляры к сторонам треугольника ABC
По теореме Пифагора для треугольников PAK и PBK
PK^2 =PA^2 -AK^2 =PB^2 -BK^2 <=> PA^2 -PB^2 =AK^2 -BK^2
(Доказали, что разность квадратов наклонных равна разности квадратов их проекций.)
PB^2 -PC^2 =BL^2 -CL^2
PC^2 -PA^2 =CM^2 -AM^2
Сложим:
AK^2 -BK^2 +BL^2 -CL^2 +CM^2 -AM^2 =0 <=>
AK^2 +BL^2 +CM^2 =CL^2 +BK^2 +AM^2
Если перпендикуляры к сторонам пересекаются в одной точке, то выполняется это равенство.
(Обратное док-во: разность квадратов наклонных для двух пересекающихся перпендикуляров подставляем в доказанное равенство - получаем разность квадратов наклонных для третьего отрезка - тогда он также является перпендикуляром.)
Проверим данные из условия
AK=BK=6, BL=AM=1
CM= {9, 11}
CL= {7, 9}
CM^2 =CL^2 в одном случае:
точка M на стороне, точка L на продолжении стороны.
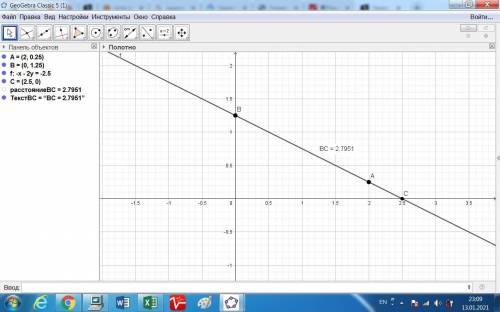
Дана точка A(2; 0,25) и прямая, проходящая через эту точку и пересекающаяся с положительными полуосями в точках B и С.
Найти уравнение прямой, для которой отрезок ВС будет минимальным.
Эта задача имеет 2 решения:
- 1) миниминизация длины отрезка ВС с применением теоремы Пифагора для треугольника с катетами ОВ и ОС,
- 2) те же действия с использованием критического угла наклона отрезка к оси Оу при его минимальной длине.
1) Пусть ордината точки В равна "b", а абсцисса точки С равна "а".
Из подобия треугольников и координат точки А имеем:
b/0,25 = a/(a - 2), отсюда получаем соотношение для "b":
b = 0,25a/(a - 2).
Получаем функцию зависимости длины L отрезка ВС от одного из параметров:
L = √(a² + b²) = √(a² + (0,25a/(a - 2))²).
Для определения минимума функции нужно найти производную этой функции и приравнять нулю.
dL/da = (a(a³ - 6a² + 12a - 8,125))/((a - 2)³*√(0,0625/(a - 2)²) + 1)*a²)).
Приравниваем нулю числитель, решением кубического уравнения есть величина а = 2,5.
Тогда b = 0,25*2,5/(2,5 - 2) = 1,25.
Получаем минимальную длину ВС = √(1,25² + 2,5²) = √7,8125.
Поучаем: L = 2,795084972.
2) Для этого варианта есть готовая разработка решения.
Минимальная длина находится сразу по формуле:
L = (a^(2/3) + b^(2/3))^(3/2).
Подставив в формулу a = 2 и b = 0,25, получаем результат:
2 2 0,25
1,107148718 0,894427191 0,447213595
63,43494882 2,236067977 0,559016994 = 2,795084972.
По полученным a и b находим уравнение прямой.
у = -(b/a)x + b = -(1,25/2,5) x+ 1,25 = -0,5x + 1,25.
Решение аналогичной задачи, в которой выведена данная формула приведено во вложении.
2. Сумма углов в четырехугольнике равна 360 градусов. Значит в четырехугольнике ВОАD:
угол В + угол О + угол А + угол D = 360
90 + 105 + 90 + угол D = 360
угол D = 360 - 285
угол D = 75 градусов
ответ: 75 градусов