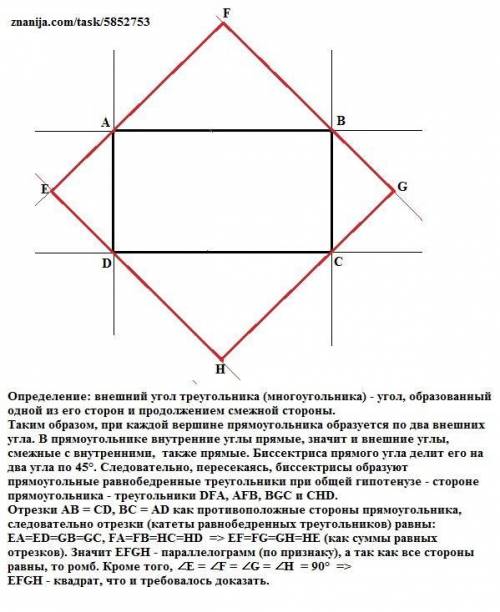
Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
1) ∠ADC+∠BCD=180º (как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD);
2) так как точка O — точка пересечения биссектрис углов трапеции, то ∠ODF+∠OCF=1/2∙(∠ADC+∠BCD)=90º;
3) так как сумма углов треугольника равна 180º, то в треугольнике COD ∠COD=90º;
4) таким образом, треугольник COD прямоугольный, а OF — высота, проведенная к гипотенузе, CF и FD — проекции катета OC и OD на гипотенузу.
5) треугольник СОD (по теореме Пифагора):
CD^2 = CO^2 + OD^2
CD = корень [CO^2 + OD^2] = корень [3^2 + 4^2] = 5
6) Обозначим CF = m
тогда FD = 5-m
OF = r (радиус)
Треугольник СFО (по теореме Пифагора):
r^2 + m^2 = OC^2
r^2 + m^2 = 3^2
откуда r^2 = 9 - m^2
7) Треугольник ОFD (по теореме Пифагора):
r^2 + (5-m)^2 = OD^2
r^2 + (5-m)^2 = 4^2
Подставим из 6):
9 - m^2 + (5-m)^2 = 4^2
9 - m^2 + 5^2 - 2*5*m + m^2 = 4^2
9 + 25 - 10m = 16
10m = 18
m = 1.8
8) Подставим результат в 6):
r^2 = 9 - m^2 = 9 - 1,8^2 = 5,76
9) площадь круга S = П*r^2 = 5,76П ~ 18,096
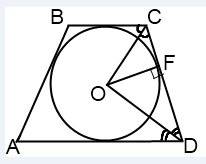
Доказательство в объяснении.
Объяснение:
Определение: внешний угол треугольника (многоугольника) - угол, образованный одной из его сторон и продолжением смежной стороны.
Таким образом, при каждой вершине прямоугольника образуется по два внешних угла. В прямоугольнике внутренние углы прямые, значит и внешние углы, смежные с внутренними, также прямые. Биссектриса прямого угла делит его на два угла по 45°. Следовательно, пересекаясь, биссектрисы образуют прямоугольные равнобедренные треугольники при общей гипотенузе - стороне прямоугольника - треугольники DFA, AFB, BGC и CHD.
Отрезки АВ = CD, BC = AD как противоположные стороны прямоугольника, следовательно отрезки (катеты равнобедренных треугольников) равны: EA=ED=GB=GC, FA=FB=HC=HD => EF=FG=GH=HE (как суммы равных отрезков). Значит EFGH - параллелограмм (по признаку), а так как все стороны равны, то ромб. Кроме того, ∠E = ∠F = ∠G = ∠H = 90° =>
EFGH - квадрат, что и требовалось доказать.