Объяснение:
1) Утверждение неверно.
Если площадь одного из подобных треугольников в 2 раза больше площади другого, то коэффициент подобия равен k = √2, потому что отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2) Утверждение верно.
а) Если боковая сторона трапеции равна меньшему основанию, то диагональ его является биссектрисой острого угла, образованного большим основанием и этой боковой стороной.
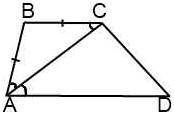
Смотри прикреплённый рисунок 1.
Так как AB = BC, то Δ ABC — равнобедренный с основанием AC. Значит, ∠BAC = ∠BCA.
∠BCA = ∠CAD (накрест лежащие углы при AD ∥ BC и секущей AC).
Тогда ∠BAC = ∠CAD, и AC - биссектриса ∠BAD.
б) Если боковая сторона трапеции равна большему основанию, то диагональ его является биссектрисой тупого угла трапеции, образованного меньшим основанием и этой стороной.
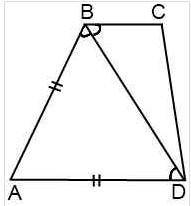
Смотри прикреплённый рисунок 2.
АВ = АD и ΔABD — равнобедренный с основанием BD, его углы при основании равны ∠ABD = ∠ADB.
∠CBD = ∠ADB (накрест лежащие при AD ∥ BC и секущей BD).
Тогда ∠CBD=∠ABD, следовательно, BD — биссектриса ∠ABC.
3) Утверждение верно,
Вписанный угол АВС опирается на дугу окружности, равную 288°, а центральный угол АОС опирается на дугу окружности, равную 360 ° - 288° = 72°.
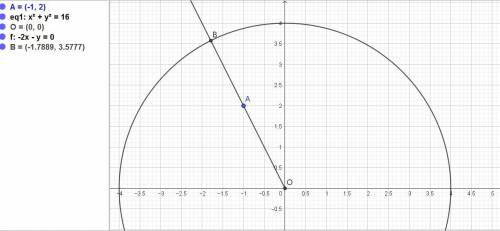
Даны точка А(-1; 2) и кривая x² + y² = 16.
Квадрат расстояния между двумя точками определяется соотношением d²=(x1−x2)²+(y1−y2)². Так как надо найти расстояние от точки до кривой, то координаты второй точки (лежащей на кривой) должны удовлетворять ее уравнению, поэтому d²=(x1−x2)²+(y1−f(x2))²=
= (x + 1)² + (√(16 - x²) - 2)² = x² + 2x + 2 + 16 - x² - 4√(16 - x²) + 4 =
= 2x −4√(16 - x²) + 20.
Расстояние от точки до кривой - это минимальное расстояние между двумя точками, одна их которых лежит на кривой. Тогда для нахождения расстояния нам надо найти минимум функции определяющей расстояние, то есть, найти ее производную и приравнять нулю.
(d²)′ = 2(√(16 - x²) + 2x) / √(16 - x²).
Приравняем нулю числитель (можно выражение в скобках).
√(16 - x²) + 2x = 0 или √(16 - x²) = -2x.
Отсюда вывод: знак переменной х отрицателен.
Возведём обе части в квадрат.
16 - x² = 4x²,
5x² = 16, отсюда х = +- 4/√5, но у нас х = -4√5.
Находим у = +-√(16 - x²), но так как точка А имеет ординату с плюсом, то и ближайшая точка на кривой тоже с плюсом.
у = √(16 - (-4/√5)²) = √(16 - (16/5)) = √(64/8) = 8/√5.
Расстояние находим по вышеприведенной формуле.
d² = (-4/√5) - (-1))² + (8/√5 - 2)² = 21 - 8√5.
d = √(21 - 8√5) = √(16 - 8√5 + 5) = √(4 - √5)² = 4 - √5 ≈ 2,236.
Эту задачу можно было решить проще.
Заданная кривая x² + y² = 16 это окружность с центром в начале координат и радиусом 4.
Ближайшая точка лежит на одном радиусе ОА.
ОА = √(-1 - 0)² +(2 - 0)² = √5.
ответ: d = 4 - √5.