8 / ![\sqrt[n]{3}](/tpl/images/1337/3995/c878f.png)
и 4 *
Объяснение:
Назвемо точку перетину меншой висоти та сторони AD - K
Розглянемо трикутник ABK
кут AKB = 180 - (90 + 60) = 30
Використаємо теорему синусів:
4 / /2 = сторона DK / 1/2
сторона DK = 4 /
За властивістю прямокутного трикутника - сторона, що лежить проти кута 30 градусів вдвічі менша за гіпотенузу, тобто
AB = 8 /
Те ж саме з трикутником BCN(N - точка перетину більшой висоти зі стороною CD)
Використаємо теорему синусів:
6 / /2 = NC / 1/2
NC = 2 *
За властивістю прямокутного трикутника - сторона, що лежить проти кута 30 градусів вдвічі менша за гіпотенузу, тобто
BC = 4 *
Відповідь: 8 / и 4 *
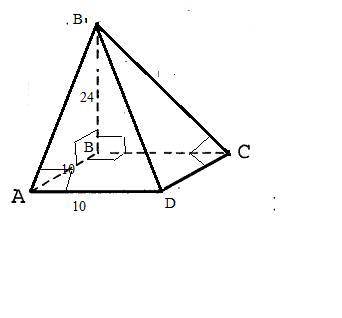
Основанием пирамиды является квадрат со стороной 10 см. Одно боковое ребро перпендикулярно плоскости основания и равно 24 см.
Вычисли площадь боковой поверхности.
Объяснение:
1)S(бок)=S(МВА)+S(МВС)+S(МАD)+S(МСD).
2)ΔМВА=ΔSМВС как прямоугольные по двум катетам⇒S(МВА)=S(МВС)=1/2*24*10=120 (см²).
Найдем МС= МА=√(24²+10²)=√676=26(см)
3)Т.к. прекция ВА⊥AD, то и наклонная МА⊥AD⇒ΔМAD-прямоугольный.
Т.к. прекция ВС⊥СD, то и наклонная МС⊥СD⇒ΔМСD-прямоугольный.
S(МАD)=S(МСD) как площади равных прямоугольных треугольников по катету и гипотенузе .
S(МАD)=S(МСD)=1/2*10*26=130 (см²)
4)S(бок)=2*120+2*130=500 (см²)
но она и не пригодилась...
1/ отрезки касательных, проведенных из одной точки (К) равны...
DK=KC
2/ центр вписанной в угол окружности лежит на биссектрисе этого угла))
ОК - биссектриса ∠DKC
∠DKO = ∠CKO
∠DOK = ∠COK
3/ вписанный угол равен половине градусной меры центрального, опирающегося на ту же дугу
∠DAC (опирается на дугу DC) = (1/2)∠DOC = ∠KOC
т.е. DA || KO
О --середина АС ---> KO --средняя линия, К --середина ВС
DK = KC = (1/2)BC = 6