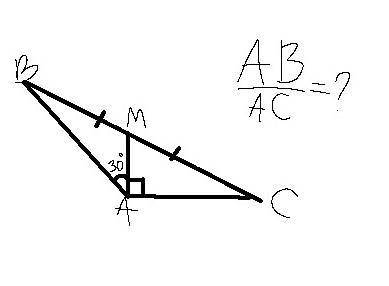
Смотрите на рисунок ...
У сторон АВ и АС общая вершина - А, и через неё и проведём медиану АМ к стороне ВС ...
Будем искать:
АС/АВ = ?
ИЛИ
АВ/АС = ?
Итак ...
Что можно сказать про медиану?
Она делит треугольник на два треугольника, площади которых равны ...
Получаем :
1) Площадь треугольника АВМ = площадь треугольника АМС.Рассмотрим треугольник ВМА.
Его площадь можно найти по вот такой формуле:
Площадь треугольника ВМА = ½*АВ*АМ*синус угла ВАМ
По условию угол ВАМ равен 30° ...
Площадь треугольника ВМА = ½*АВ*АМ*синус угла в 30°
Синус в 30° равен ½.
Получаем:
Площадь треугольника ВМА = ¼*АВ*АМ.
Теперь посмотрим на треугольник АМС.
Он прямоугольный... А площадь прямоугольного треугольника равна половине произведения его катетов. (В нашем случае АМ и АС - катеты).
Запишем вот так :
Площадь треугольника АМС = ½*АС*АМ..
ПО ВЫШЕ СКАЗАННОМУ В ПУНКТЕ 1 СЛЕДУЕТ, ЧТО :
½*АВ*АМ = ¼*АМ*АС
½*АВ = ¼*АС
АВ = ½*АС ...
Получаем :
АС/АВ = АС/(½*АС) = 1 : ½ = 2.
АВ/АС = (½*АС)/АС = ½.
(ЕСЛИ НЕВЕРНО ОТМЕТЬТЕ КАК НАРУШЕНИЕ!)
Смотрите на рисунок ...
У сторон АВ и АС общая вершина - А, и через неё и проведём медиану АМ к стороне ВС ...
Будем искать:
АС/АВ = ?
ИЛИ
АВ/АС = ?
Итак ...
Что можно сказать про медиану?
Она делит треугольник на два треугольника, площади которых равны ...
Получаем :
1) Площадь треугольника АВМ = площадь треугольника АМС.Рассмотрим треугольник ВМА.
Его площадь можно найти по вот такой формуле:
Площадь треугольника ВМА = ½*АВ*АМ*синус угла ВАМ
По условию угол ВАМ равен 30° ...
Площадь треугольника ВМА = ½*АВ*АМ*синус угла в 30°
Синус в 30° равен ½.
Получаем:
Площадь треугольника ВМА = ¼*АВ*АМ.
Теперь посмотрим на треугольник АМС.
Он прямоугольный... А площадь прямоугольного треугольника равна половине произведения его катетов. (В нашем случае АМ и АС - катеты).
Запишем вот так :
Площадь треугольника АМС = ½*АС*АМ..
ПО ВЫШЕ СКАЗАННОМУ В ПУНКТЕ 1 СЛЕДУЕТ, ЧТО :
½*АВ*АМ = ¼*АМ*АС
½*АВ = ¼*АС
АВ = ½*АС ...
Получаем :
АС/АВ = АС/(½*АС) = 1 : ½ = 2.
АВ/АС = (½*АС)/АС = ½.
(ЕСЛИ НЕВЕРНО ОТМЕТЬТЕ КАК НАРУШЕНИЕ!)

АВС, АСД и АВД.
Треугольник АВС примем в прямоугольной системе координат точкой А в начало и точкой В - по оси Ох.
А(0; 0), В(7; 0).
Из первого по теореме косинусов находим косинусы углов А, В и С.
Отрезки СД и ВД по заданию равны:
СД = 6*(7/8) = 21/4 = 5,25.
ВД = 6*(1/8) = 3/4 = 0,75.
cos A= (АВ²+АС²-ВС²)/(2*АВ*АС) = 0,52381.
A = 1,019479 радиан = 58,41186 градусов.
cos В= (АВ²+ВС²-АС²)/(2*АВ*ВС) = 0,904762.
B = 0,439976 радиан = 25,20877 градусов.
cos C= (АC²+ВС²-АВ²)/(2*АC*ВС) = -0,111111 = -1/9.
C = 1,682137 радиан = 96,37937 градусов.
Хс = АС*cos A = 3*0,52381 = 1,571429.
Yc =AC*sin A = 3*√(1-0,52381²) = 3* 0,851835 = 2,555506.
Сторона АД = √(3²+5,25²-2*3*5,25) = 6,3294945.
Аналогично находим координаты точки Д.
Хд = 6,321429.
Yд = 0,319438.
Находим координаты центров О1 и О2 окружностей, вписанных в треугольники АСД и АВД.
Хо1 = (CD*Ха+АС*Хd+АD*Хс)/ Р = 1,982965.
Уо1 = (CD*Уа+АС*Yd+АD*Ус)/ Р = 1,17517.
Хо2 = (ВD*Ха+АB*Хd+АD*Хb)/ Р = 6,28975.
Уо2 = (ВD*Уа+АB*Yd+АD*Уb)/ Р = 0,158817.
Здесь Р - периметр треугольника.
Находим площади треугольников по формуле Герона:
S(ACD) = 7,826238.
S(ABD) = 1,11803.
Находим радиусы вписанных окружностей:
r1 = S(ACD)/p = 7,826238/ 7,2897472 = 1,073595.
r2 = S(ABD)/p = 1,11803/ 7,039747225 = 0,158817.
Теперь находим длину L отрезка О1О2:
L = √(Хо2-Хо1)²+(Уо2-Уо1)²) = 4,425080879.
По Пифагору находим:
EF = √(L²-(r1+r2)²) = 4,25.