Проведите прямую , обозначьте её буквой а и отметьте точку а и в лежащие на этой прямой и точки p q и r не лежащий на ней. опишите взаимное расположение точек a,b,p,q,r и прямой a

👇

Ответ:

Nastya90Lapka

15.05.2022

Решение задания смотри на фотографии
Проведите прямую , обозначьте её буквой а и отметьте точку а и в лежащие на этой прямой и точки p q

4,4(56 оценок)

Открыть все ответы

Ответ:

pjs

15.05.2022

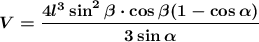
$\boldsymbol{V=\dfrac{4l^3\sin^2\beta\cdot \cos\beta (1-\cos\alpha)}{3\sin\alpha}}$

Объяснение:

Центр окружности, вписанной в равнобедренную трапецию, лежит на середине отрезка КЕ (точки К и Е - середины оснований).

Так как точка пересечения диагоналей лежит на том же отрезке, но ближе к меньшему основанию, высота пирамиды лежит на образующей конуса, проходящей через точку К.

Высота трапеции равна диаметру вписанной окружности, а суммы противолежащих сторон равны.

Итак, ВР = КЕ = 2R,

AB + CD = AD + BC

AD = b, BC = a.

Чтобы найти высоту пирамиды, надо знать длину КН, а для этого найти расстояние между центром окружности и основанием высоты пирамиды ОН = х.

ΔАВР: ∠АРВ = 90°,

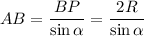
$AB=\dfrac{BP}{\sin\alpha}=\dfrac{2R}{\sin\alpha }$

AP = BP · ctg α = 2R · ctg α

Тогда

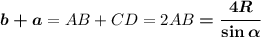
$\boldsymbol{b+a}=AB+CD=2AB\boldsymbol{=\dfrac{4R}{\sin\alpha}}$

Так как по свойству равнобедренной трапеции

АР = (AD - BC) / 2, то

b - a = 2AP = 4R · ctg α

ΔAHD ~ ΔCHB по двум углам, тогда их высоты относятся как сходственные стороны:

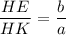
$\dfrac{HE}{HK}=\dfrac{b}{a}$

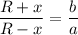
$\dfrac{R+x}{R-x}=\dfrac{b}{a}$

a(R + x) = b(R - x)

aR + ax = bR - bx

x(a + b) = R(b - a)

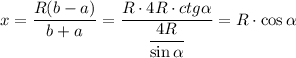
$x=\dfrac{R(b-a)}{b+a}=\dfrac{R\cdot 4R\cdot ctg\alpha}{\dfrac{4R}{\sin\alpha}}=R\cdot \cos\alpha$

KH = R - x = R(1 - cos α)

Справа на рисунке осевое сечение конуса, проходящее через хорду КЕ.

∠KSH = ∠KMO = β как соответственные при SH║MO и секущей КМ.

SH = KH · ctg β = R(1 - cos α) · ctgβ

Итак, объем пирамиды:

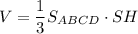
$V=\dfrac{1}{3}S_{ABCD}\cdot SH$

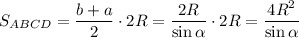
$S_{ABCD}=\dfrac{b+a}{2}\cdot 2R=\dfrac{2R}{\sin\alpha }\cdot 2R=\dfrac{4R^2}{\sin\alpha}$

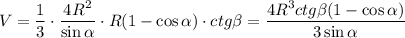
$V=\dfrac{1}{3}\cdot \dfrac{4R^2}{\sin\alpha }\cdot R(1-\cos\alpha )\cdot ctg\beta=\dfrac{4R^3ctg\beta (1-\cos\alpha)}{3\sin\alpha}$

Осталось из прямоугольного треугольника МОЕ выразить R:

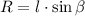
$R=l\cdot \sin\beta$

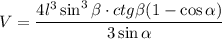
$V=\dfrac{4l^3\sin^3\beta\cdot ctg\beta (1-\cos\alpha)}{3\sin\alpha}$

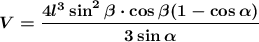
$\boldsymbol{V=\dfrac{4l^3\sin^2\beta\cdot \cos\beta (1-\cos\alpha)}{3\sin\alpha}}$

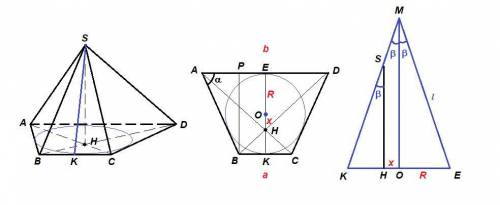
Основанием пирамиды служит равнобедренная трапеция с острым углом Эта трапеция описана около окружн

4,6(19 оценок)

Ответ:

qwerty836

15.05.2022

Вступление:

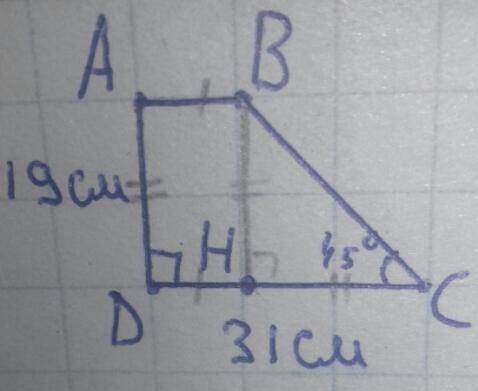
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.

H∈DC, BH⊥DC ⇒ BH=AD=19см.

В прямоугольном ΔBHC:

∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.

DH=DC-HC=31-19=12см.

В четырёхугольнике ABHD:

∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.

Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.

AB мень. осн. т.к. CD - большее.

Меньшее основание равно 12см.