1)на двух материках : в Северной и Южной Америке, западная часть обеих материков. между 66°градусов до 56° градусов
2) горы протянулись в направлении север-юг, длина приблизительно 12 000 км.
3) почти на всём протяжении является водоразделом между бассейнами Атлантического и Тихого океанов, а также резко выраженной климатической границей. Кордильеры лежат во всех географических поясах (кроме субантарктического и антарктического) и отличаются большим разнообразием ландшафтов и ярко выраженной высотной поясностью. Снеговая граница на Аляске - на высоте 600 м, на Огненной Земле -500-700 м в Боливии и Южном Перу поднимается до 6000-6500 м. В северо-западной части Кордильер Северной Америки и на юго-востоке Анд ледники спускаются до уровня океана, в жарком поясе они покрывают лишь наиболее высокие вершины. Общая площадь оледенений -около 90 тысяч км (в Кордильерах Северной Америки - 67 тыс. км в Андах -около 20 тыс. км)))
ответ: 6,6
Вариант решения.
Формула площади треугольника S=a•h/2 => h=2S:a.=>
Чем больше сторона треугольника, тем меньше высота, которая к ней проведена.
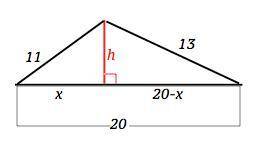
Пусть высота, проведенная к стороне 20, делит ее на отрезки х и 20-х, и образует два прямоугольных треугольника, гипотенузы которых - другие стороны исходного треугольника.
Выразим квадрат высоты из 1-го треугольника по т.Пифагора:
h²= 11²-х²
Аналогично – то же из второго треугольника:
h²=13²-(20-x)²
Приравняем эти значения
11²-х²=13²-(20-x)² Решив уравнение, получим
40х=352
х=8,8
Из меньшего треугольника по т.Пифагора
h=√(121-77,4)= 6,6 ( ед. длины)
Пусть АС=х, тогда АВ=ВС=(20-х): 2
Рассмотрим треугольник АВМ - прямоугольный, угол М прямой:
АВ=(20-х): 2, ВМ=6, АМ=х: 2
По теореме Пифагора: к^2+к^2=г^2:
Подставляем значения сторон:
(х: 2)^2+6^2=((20-х): 2)^2
После возведения в квадрат избавляемся от знаменателей, умножив все члены уравнения на 4, получаем:
х^2+144=400-40х+х^2
Переносим иксы влево, числа - вправо, сокращаем противоположные числа, получаем:
40х=400-144
40х=256
Делим все на 40:
х=6.4
Подставляем икс в значения длин сторон треугольника АВС.
ответ:
АВ=ВС=6.8
АС=6.4