Верное решение уже дано. И желательно помнить данные в нем отношения проекций катетов к частям гипотенузы.
Теорема (о соотношениях в прямоугольном треугольнике).
В прямоугольном треугольнике справедливы следующие соотношения:
1) h2 = a1 · b1;
2) b2 = b1 · c;
3) a2 = a1 · c,
где b1 и a1 - проекции катетов b и a на гипотенузу с.
Но можно задачу решить несколько иначе, хотя это решение будет подлиннее.
Из подобия треугольников, образованных высотой, катетами и их проекцией на гипотенузу составить пропорцию, обозначив высоту треугольника х.
Тогда х, деленный на проекцию большего катета равен отношению проекции меньшего катета на х:
Повторю, что за х берем высоту треугольника:
х:18=6:х
Получим х²=18*6
х=√108=6√3
Теперь по теореме Пифгора больший катет найдем.
Катет = √(6√3)²+18²=12√3 см
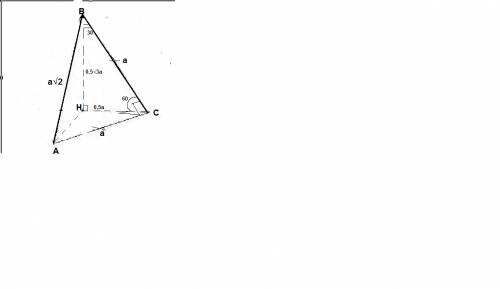
1) Экскурс в теорию: угол между плоскостями (ВАС) и (САН)- двугранный угол (НАСВ) измеряется градусной мерой линейного угла L HCB , образованного лучами СВ и СН , имеющими начало на ребре (АС) и перепендикулярными к нему,
т.е. L HCB = 60⁰. (см. рис.).
2) Углом между прямой.... и плоскостью наз-ся угол между этой прямой и её проекцией на данную плоскость, тогда углом между катетом ВС и плоскостью (САН) является L L HCB = 60⁰ .
3) Угол между гипотенузой АВ найдём, рассмотрев ΔАВН - прям.:
sin L BAH = BH/AB = 0,5√3a/(a√2) =√6/4,
таким образом L BAH = arcsin √6/4.
ОТвет: 60⁰; arcsin √6/4.
/
3 / 4
/
5/ 6
/
7 / 8
Пусть угол 1=48 градусов, тогда вертикальный с ним угол 3 тоже равен 48 градусов по свойству вертикальных углов. А угол 2 смежный с 1. Он равен 180-48=132 градуса. Вертикальный с ним угол 4 равен тоже 132 град по свойству вертикальных углов. И наконец равны соответственные и накрест лежащие углы для нижней прямой:
угол6=углу7=132 градуса и угол 5= углу 8 = 48 градусов