Объяснение:
№1
Чтобы найти нам площадь ABCD нам надо найти высоту BH и основание AD.
1. Рассмотрим ∆ABH: sinA=BH/AB
1/2=BH/8
отсюда BH=4;
2. AD=AH+HD
cis30°=AH/AB
√(3)/2=AH/8
8√(3)=2AH
AH=4√(3)
Отсюда AD=12+4√(3)≈19
3. Площадь ABCD=BH*AD=4*19=76см².
№2
Задача. Дан параллелограмм ABCD, боковая сторона равна 4 см, диагональ соединяющая вершины тупых уголов равна 5 см и перпендикулярна к боковым сторонам. Найдите основания параллелограмма.
Диагональ делит параллелограмм на 2 прямоугольных ∆ABD и ∆BDC.
Рассмотрим ∆ABD:
По теореме Пифагора:
AD²=AB²+AD²
AD²=16+25
AD²=41
AD=√(41)
Объяснение:
Дано: треугольник АВС, АВ=ВС, О-середина АС. а) Постройте фигуру, симметричную треугольнику АВС относительно точки О. б) Какую фигуру вместе образуют треугольник АВС и ему симметричный?
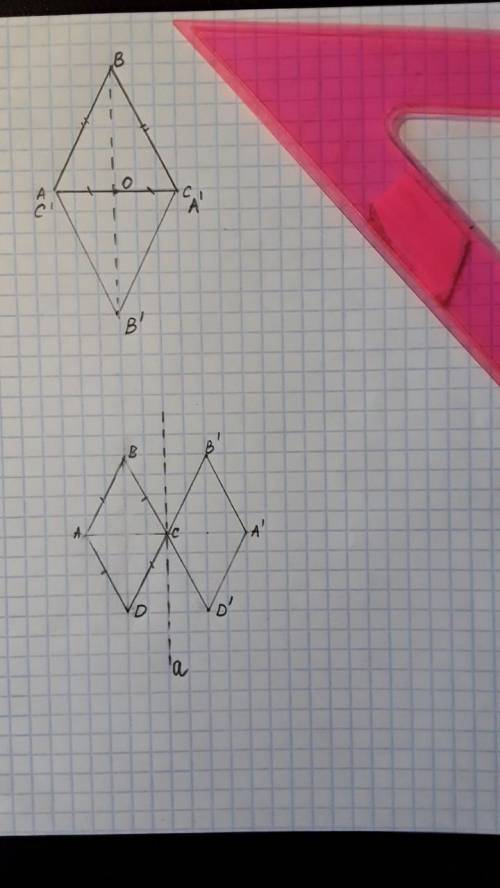
Решение 1а в приложении .
При центральной симметрии В→В’ , А→А ’=С , С→С ’=А
б)Треугольник АВС и ему симметричный образуют ромб , тк АВ=С’В’ , ВС=А’В’ .
№2
Постройте ромб АВСD. Постройте фигуру, симметричную ромбу относительно прямой, проходящей через точку С и параллельной ВD. В какую фигуру перейдет ромб АВСD при этой симметрии?
Решение 2 в приложении .
Прямая а║ВD, С∈а
При осевой симметрии ромб АВСD перейдет ромб А’В’СD’.
Точка С отобразится сама в себя.
∠ABC = 180° - ∠A - ∠C = 180° - 30° - 60° = 90° ⇒
ΔABC - прямоугольный.
BC - катет, лежащий против угла 30°, равен половине гипотенузы ⇒
AC = BC * 2 = 7 * 2 = 14 см
ΔBHC : ∠BHC = 90°; ∠C = 60° ⇒ ∠CBH = 90° - 60° = 30°
HC - катет, лежащий против угла 30° ⇒
HC = 1/2 BC = 1/2 * 7 = 3,5 см
AH = AC - HC = 14 - 3,5 = 10,5 см