1. Верно (свойство радиуса, проведённого в точку касания).
2. Неверно. Вписанный угол равен половине центрального соответствующего угла.
3. Неверно. Вписанный угол, опирающийся на полуокружность, равен 90° (так как полуокружность — это дуга в 180°, а градусная мера вписанного угла измеряется половиной градусной меры соответвующией дуги. Откуда вписанный угол равен 180° : 2 = 90°).
4. Верно (теорема о пересекающихся хорд в окружности).
5. Верно. Если расстояние от центра окружности до прямой больше радиуса, то у этой прямой и окружности нет общих точек.
7,499 см (расстояние от центра окружности до прямой) > 7,49 см (радиус окружности). Поэтому, по выше сказанному, у окружности и прямой нет общих точек.
6. Неверно. Такая дуга равна 30°*2 = 60° (смотрите в пункт 3).
7. Верно (свойство отрезков касательных, проведённых из одной точки).
8. Верно (по определению радиуса окружности).
9. Неверно. Прямая называется секущей по отношению к окружности только тогда, когда она имеет с окружностью две общие точки).
10. Верно (свойство касательных).
1. Верно (свойство радиуса, проведённого в точку касания).
2. Неверно. Вписанный угол равен половине центрального соответствующего угла.
3. Неверно. Вписанный угол, опирающийся на полуокружность, равен 90° (так как полуокружность — это дуга в 180°, а градусная мера вписанного угла измеряется половиной градусной меры соответвующией дуги. Откуда вписанный угол равен 180° : 2 = 90°).
4. Верно (теорема о пересекающихся хорд в окружности).
5. Верно. Если расстояние от центра окружности до прямой больше радиуса, то у этой прямой и окружности нет общих точек.
7,499 см (расстояние от центра окружности до прямой) > 7,49 см (радиус окружности). Поэтому, по выше сказанному, у окружности и прямой нет общих точек.
6. Неверно. Такая дуга равна 30°*2 = 60° (смотрите в пункт 3).
7. Верно (свойство отрезков касательных, проведённых из одной точки).
8. Верно (по определению радиуса окружности).
9. Неверно. Прямая называется секущей по отношению к окружности только тогда, когда она имеет с окружностью две общие точки).
10. Верно (свойство касательных).
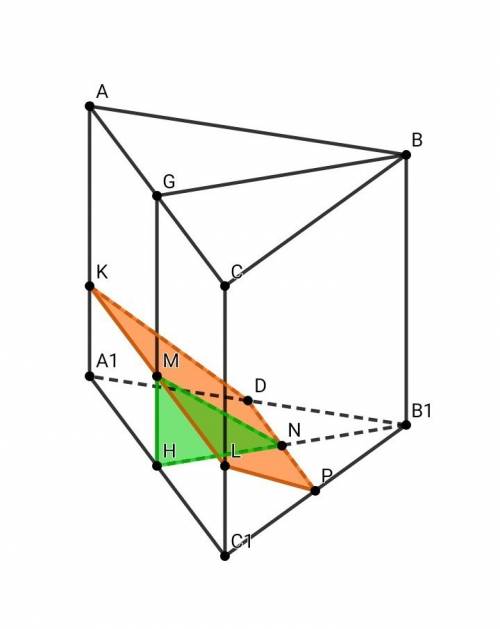
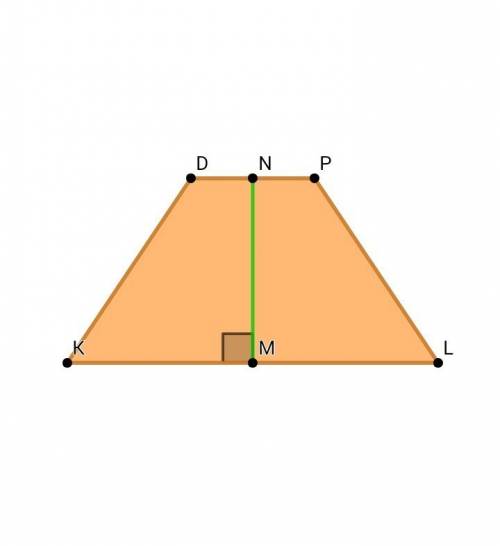
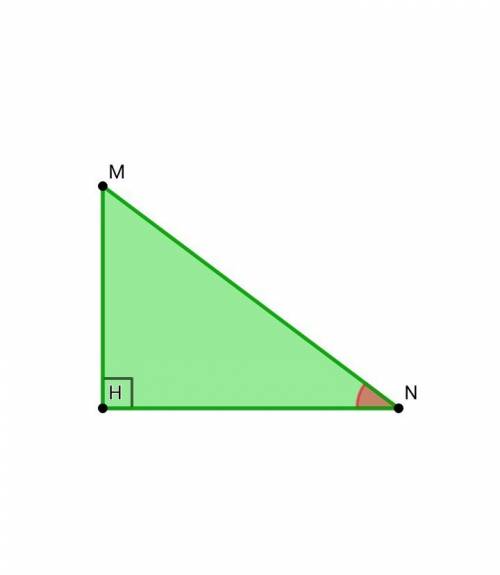
в сечении получится трапеция... (сорри за грязь на рисунке...) ее высота-гипотенуза треугольника с углом в 30°; основания =15.7 и 15.7/2 (средняя линия треугольника в основании) если остались вопросы-с удовольствием отвечу)