меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
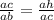
теперь подставим наши значения в эту пропорцию:
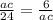
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

Объяснение:
гипотенуза с=25см
1 катет а=х
2 катет b=(x+5)
по теореме Пифагора
а²+b²=c²
x²+(x+5)²=25²=625
составим уравнение
x²+(x+5)²-625=0
x²+x²+10x+25-625=0
2x²+10x-600=0
дискриминант
D=b²-4ac=10²-4×2×(-600)=100+4800=4900
корень
x1= -b+√D/2a= -10+√4900/2×2= -10+70/4=60/4=15
x2= -b-√D/2a= -10-√4900/2×2= -10-70/4= -80/4= -20
проверяем
15²+(15+5)²-625=225+20²-625=225+400-625=625-625=0
1 катет а=15 см
2 катет b=20см
площадь прямоугольного треугольника равна половине произведения катетов а и b .
S=1/2 ×a×b=1/2 ×15×20=150 см²
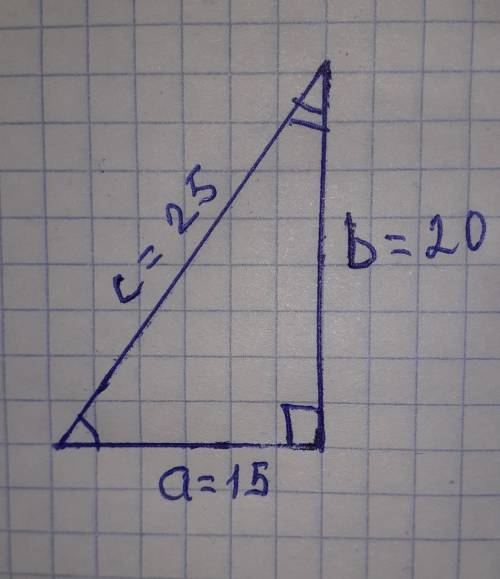
Средняя линия трапеции равна половине суммы её оснований
(9 + 7 ) \ 2 = 8 см - средняя линия