Дано:
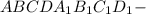 Правильная усеченная пирамида
Правильная усеченная пирамида
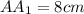 (ребро)
(ребро)
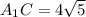 (диагональ)
(диагональ)
Найти: 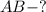
1) Проведём две высоты к плоскости ABCD из вершин 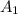 и
и 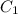 И отметим их как
И отметим их как 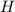 и
и 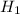 соответственно.
соответственно.
2)Рассмотрим полученный треугольник 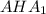 ; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна
; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна 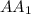 , то можно и найти
, то можно и найти 
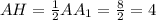 (Против угла в 30 градусов лежит катет равный половине гипотенузы).
(Против угла в 30 градусов лежит катет равный половине гипотенузы).
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем 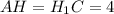
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника: 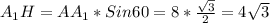
5)Следует детально рассмотреть треугольник 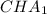 В нем известны две стороны, и он прямоугольный, а значит можно найти
В нем известны две стороны, и он прямоугольный, а значит можно найти 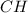 по теореме Пифагора.
по теореме Пифагора. 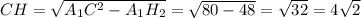 .
.
6)Отсюда можно найти 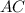 .
.
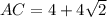 . Знаю эту величину можем найти искомую АB.
. Знаю эту величину можем найти искомую АB.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат. 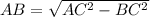 ; Но также стоит заметить, что
; Но также стоит заметить, что 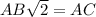 , но второй намного легче, чем мучиться с преобразованием корневых выражений.
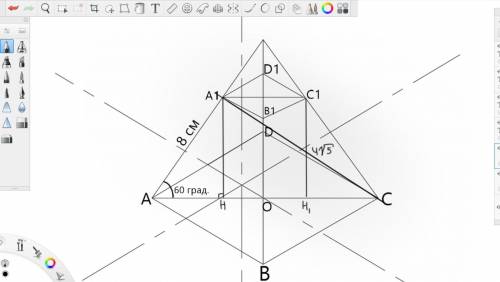
, но второй намного легче, чем мучиться с преобразованием корневых выражений. 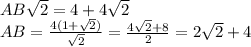
ответ: AB= двум корней из двух плюс 4
Рассмотрим сечение ЦИЛИНДРА Это прямоугольный РАВНОБЕДРЕННЫЙ треуголльник ABC (так как углы равны по 45 град. ) т.е AC=BC .По теореме Пифагора найдем эти стороны . оставим уравнение Х^2(в квадрате)+ Х^2(в квадрате)=64 ИЗ этого следует
2Х^2(в квадрате)=64 , Х^2(в квадрате)=32 , Х=32(из под коря )=4*3(из под корня )
1 А так так ВС-это и есть высота . то BC=4*3(из под корня )
2 а AC=d(диаметру) и = 4*3(из под корня ). А r(радиус )=2/d . И из этого следует
AC=4*3(из под корня)/2= 2*3(из под корня)-ЭТО РАДИУС
ответ высота BC=4*3(из под корня ), а ралиус (r)=2*3(из под корня)
Рассмотрим треугольник, образованный двумя радиусами описанной около декагона (правильного десятиугольника) окружности и его стороной. Это равнобедр. треуг. с боковыми сторонами, равными 5.
Угол между радиусами определяется так - 360°/10 = 36°.
Сторону декагона можно найти по теореме косинусов:
ответ: a₁₀ = 3.1м