Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник (свойство) => ВС=ВF=5.
AD=BC=5 (противоположные стороны параллелограмма). KD= КА+AD=4+5 = 9.
Треугольники KAF и KDC подобны (так как AF параллельна DC). Из подобия: KD/KA=CD/AF.
CD=AB, AF=x, CD=5+x. Тогда 9/4=(5+x)/x. =>
х = 4. АВ=CD=4+5=9.
Или так:
КА параллельна ВС => <CKA=<BCK как накрест лежащие. <KFA=<BFC (вертикальные)=<BCF =>
Треугольник KAF равнобедренный и AF=КА=4.
АВ=CD=5+4=9.
ответ: АВ=CD = 9. BC=AD=5.

9
Объяснение:
1.треугольники AID и CIB подобны по всем равным углам (вертикальные + накр. леж. углы)
Также треугольники ABI и DCI равны
=> AI=DI и BI=IC
=> треугольники AID и CIB равнобедренны
2. Т.к. треугольники подобны, то все отношения сторон равны 1:3
Это значит, что при составлении пропорции площадей, мы получим примерно такое отношение:
(3a * 3h):2 / (a * h):2
=>
(3a * 3h):2 / (a * h):2 =
= 3a * 3h * 2 / 2 * a * h =
2 и ah сокращается и мы получаем в результате, что отношение площадей будет равно 9
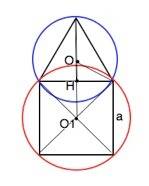
Общая хорда двух пересекающихся кругов является стороной правильного треугольника, вписанного в один круг, и стороной квадрата, вписанного в другой круг. Длина этой хорды равна a. Найдите расстояние между центрами окружностей, если они лежат по разные стороны хорды.
Обозначим центр окружности с вписанным треугольником О, центр второй - О1.
Стороны треугольника и квадрата равны а.
Искомое расстояние равно сумме расстояний ОН - от точки пересечения медиан треугольника,- до хорды- и НО1 - от хорды до точки пересечения диагоналей квадрата.
ОН равно радиусу окружности, вписанной в правильный треугольник, т.е.1/3 его высоты.
Высота =а√3/2. ОН= а√3/6
Расстояние от хорды до О1 равно половине стороны квадрата, т.е.
НО1=а/2
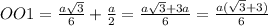
Биссектриса, проведенная из вершины параллелограмма, отсекает равнобедренный треугольник. Значит BF=BC=5.
Достроим - КВ₁ параллельно СD и продолжение ВС.
KB₁BA - параллелограмм, КС - биссектриса угла К, значит АК=АF=4. Значит АВ=AF+FB=4+5=9.