Question

Вдоль всего забора дачного участка выложили дорожку в ширину 1 каменной плитки размером 50 на 50 см. сколько каменных плиток потребовалось для укладки дорожки?
p.s.

Answer 1

ответ:38м

1)1200+1400=2600(см)

2)2600+800=3400(см)

3)3400+400=3800(см)

3800см=38м

Answer 2

100 плиток

Пошаговое объяснение:

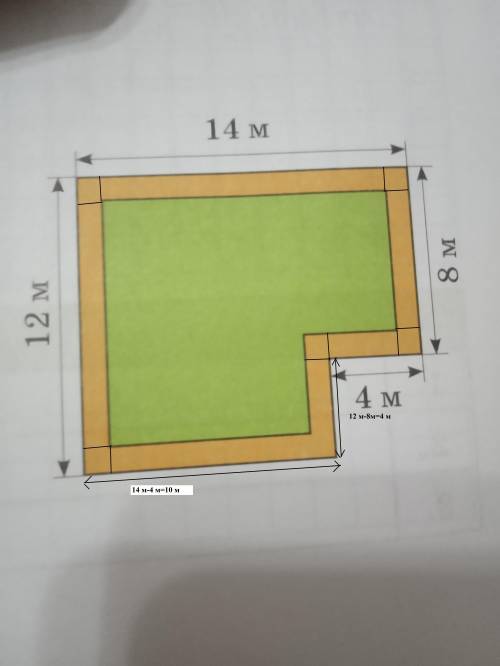
Найдем периметр всей плитки:

14 м+ 12 м+8 м+ 4 м + (12-8) м+(14-4) м=52 м

Учтем, что по углам мы одновременно учли длину и ширину плитки, а в 1 месте не учли 1 плитку:

(5-1)*50 см=200 см=2 м

52 м-2 м=50 м

Посчитаем количество плиток:

50м :50 см=5000 см:50 см=100 плиток потребуется

Answer 3

100 штук

Пошаговое объяснение:

Внимание! Данные методы решения не учитывают ширину шва между плитками. Поэтому при выполнении строительных работ вам необходимо вносить соответствующую поправку, особенно при больших площадях покрытия.

Вариант решения №1 (для начальных классов).

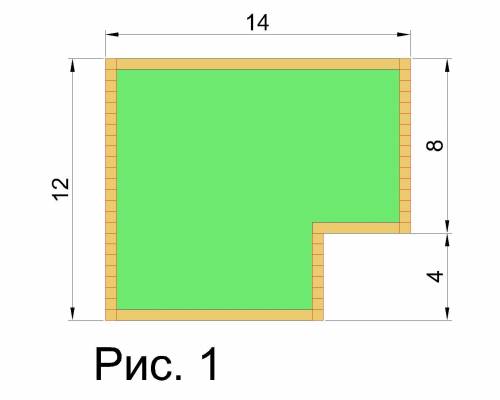
Посчитаем длину дорожки из плитки, как если бы её выложили в одну ровную полоску. Для этого вначале отсечем из фигуры вертикальные полоски, так, как это показано на рис. 1.

Получаем длину вертикальных полосок:

12+8+4=24 (м)

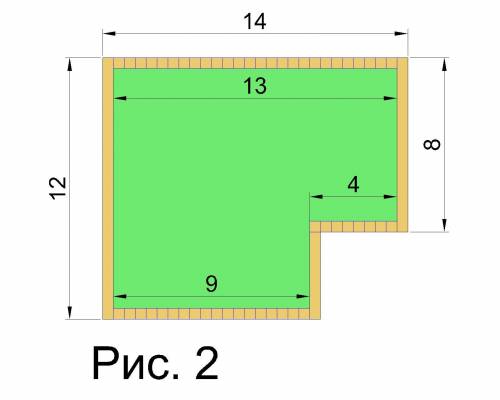
Теперь подсчитаем длину оставшихся горизонтальных полосок. Т.к. ширина плитки равна 50 см, то очевидно, что от верхней и нижней полоски вертикальные полосы "отобрали" по 50+50=100 (см), т.е. 1 м

(см. рис. 2).

Тогда

длина горизонтальных полосок:

14-1+4+(14-4)-1 = 13+4+9 = 26 (м).

Суммарная длина полосы плитки равна

24+26=50 (м) = 5000 см

Тогда количество плитки для заполнения такой полосы равно:

5000:50=100 (шт.)

Вариант решения №2 (через площадь - универсальный метод).

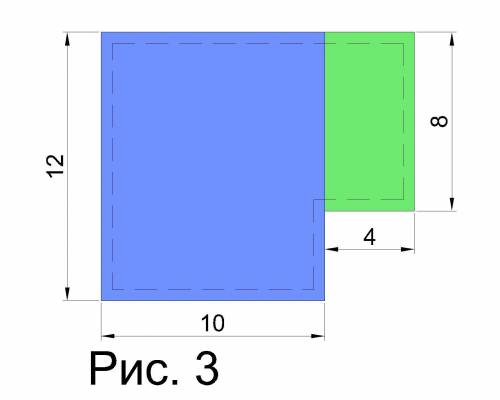
Вычислим площадь полосы плитки Sд.. Для этого из площади наружного контура Sн. вычтем площадь внутреннего контура Sв.. Площади будем вычислять как сумму площадей двух прямоугольников, как это показано на рис 3.

Sн.=Sн₁.+Sн₂=12*10+8*4=152 (м²).

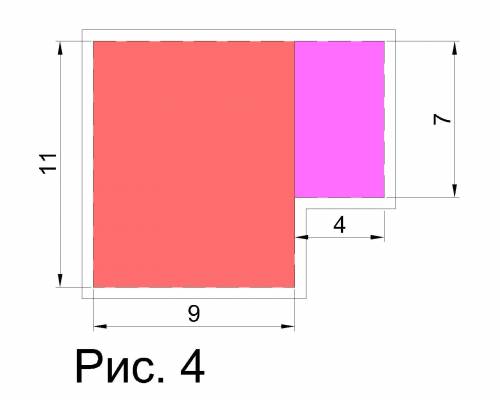
Аналогично вычислим площадь внутренней фигуры Sв. (см. рис. 4):

Sв.=Sв₁.+Sв₂=11*9+7*4=127 (м²).

Тогда площадь дорожки из плитки Sд. равна:

Sд.=Sн.-Sв.=152-127=25 (м²)

Тогда количество плиток можно найти, разделив площадь дорожки Sд. на площадь одной плитки Sп..

Sп. = 0,5*0,5=0,25 (м²)

Количество плитки равно:

Sд./Sп. =25/0,25=100 (шт.)

Вариант решения №3 (через периметр оси симметрии плитки).

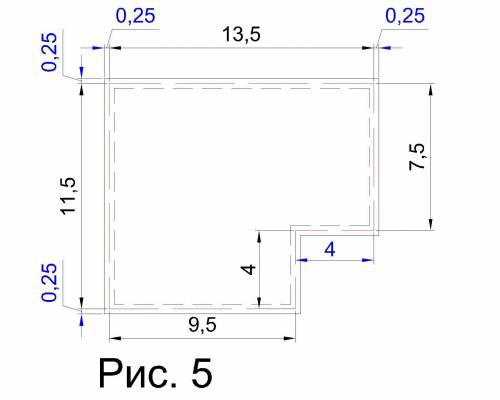
Т.к. в нашем случае плитка - уникальная, самая симметричная из четырёхугольников фигура (квадрат) и по условию задания дан (косвенно) наружный периметр фигуры, выложенной плиткой, размером 50х50 см, то очевидно, что периметр, проведённый через оси вертикальных и горизонтальных полос будет отстоять от наружного контура на 0,25 м и равен (см. рис. 5):

(12-2*0,25)+(14-2*0,25)+(8-2*0,25)+(4-0,25+0,25)+(4+0,25-0,25)+(10-2*0,25) = 11,5+13,5+7,5+4+4+9,5=50 (м)

Разделим длину осевого периметра плитки на линейный размер одной плитки:

50/0,5=100 (шт.)