На листе бумаги сначала начертили 3 пересекающиеся прямые (исходные прямые не пересекаются в одной точке), а затем 2 параллельные прямые. как могут быть расположены эти прямые, и сколько всего точек пересечения на них? (правильными могут быть несколько ответов.) 489675
Любое число от 100 до 109
Пошаговое объяснение:
Обратим внимание, что при вычитании из числа суммы его цифр получаем число, которое делится на 9.
Пойдем с конца: покажем, что последнее число - эта цифра.
Пусть последнее число X и
здесь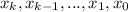 - цифры числа X. По условию
- цифры числа X. По условию
После раскрытия скобку и упрощения получим:
Но все числа в скобке положительные и поэтому сумма равна 0 тогда и только тогда, когда
Тогда X ≡ x₀, то есть цифра!
Каждый раз рассматривается разность некоторого числа и с суммой его цифр. Покажем что все разности делятся на 9. Пусть разность Y получено в некотором шаге и
Рассмотрев разность как выше получим:
которое равносильно равенству
Отсюда очевидно, что последняя сумма и в силу этого разность делится на 9. Отсюда, и числа получаемые на каждом шаге делятся на 9!
Так как из однозначных чисел делится на 9 только 9, то на 11-шаге рассматривается разность 9-9=0.
Следующее число при вычитании суммы его цифр должно давать 9, такое число 18 (10-шаг). Следующие числа:
27 (9-шаг); 36 (8-шаг); 45 (7-шаг); 54 (6-шаг); 63 (5-шаг); 72 (4-шаг); 81 (3-шаг).
Число 81 можно получить из числа 90 (90-(9+0)=81) или 99 (99-(9+9)=81).
Но число 90 нельзя получить таким Следовательно, следующее за числом 81 будет число 99 (2-шаг).
А число 99 можно получить из чисел от 100 до 109 (1-шаг: первое число).