36
Пошаговое объяснение:
Первый Второй
Так как график квадратичной функции симметричен относительно оси Oy, то площадь всей фигуры можно найти как удвоенную площадь одной из половин, например правой:
36
Пошаговое объяснение:
Первый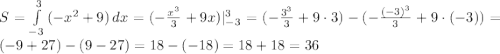 Второй
Второй
Так как график квадратичной функции симметричен относительно оси Oy, то площадь всей фигуры можно найти как удвоенную площадь одной из половин, например правой: