507. Дано: ΔABC, CH і AT — висоти, AB = 8 см, ВС = 6 см, СН = 3 см. Знайти АТ.
Площа трикутника рівна половині добутку сторони на висоту, проведену на цю сторону.
Знайдемо площу трикутника ΔABC:
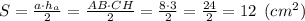
Виразимо іншу висоту через цю ж формулу:
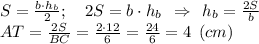
Відповідь: АТ = 4 см.
508. Дано: ΔEFS — рівнобедрений, EF — основа, EF = 40 см, SF = 29 см. Знайти S(EFS).
SF = SE = 29 см, так як ΔEFS — рівнобедрений.
Проведемо висоту SH до основи тр-ка. Висота у рівнобедреному тр-ку є медіаною, тому EH = FH = 40/2 = 20 см.
Знайдемо катет SH з ΔESH (∠EHS = 90°) за т. Піфагора:
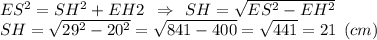
Підставимо значення у формулу площі трикутрина:
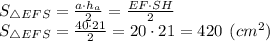
Відповідь: Площа ΔEFS рівна 420 см².

Нужно уметь переводить обыкновенные дроби в десятичные. Это можно сделать:
1) делением числителя на знаменатель на уголок;
2) домножив числитель и знаменатель на такое число, чтобы в знаменателе получались 10, 100, 1000, ...
Можно и запомнить следующие равенства (часто используются):
1/2 = 0,5; 1/4 = 0,25; 1/8 = 0,125; 2/5 = 4/10 = 0,4.
Поэтому:
1) 8 целых 1/2 + 1 целую 2/5 = 8,5 + 1,4 = 9,9;
2) 10 целых 1/4 - 6 целых 1/5 = 10,25 - 6,2 = 4,05;
3) 11 целых 5/8 + 8 целых 101/125 = 11,625 + 8,808 = 20,433;
4) 21 целая 15/16 - 19 целых 3/125 = 21,9375 - 19,024 = 2,9135, т. к.
15/16 = 75/80 = 375/400 = 1875/2000 = 9375/10000 =0,9375.