Пошаговое объяснение:
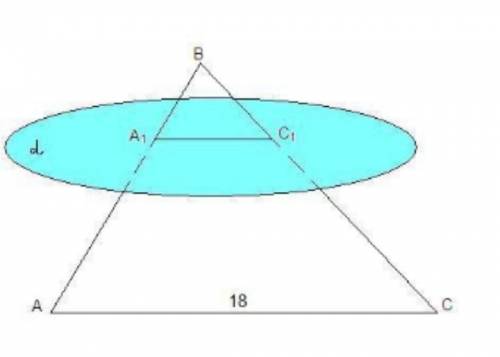
Плоскость α, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках А₁ и С₁ соответственно. Найдите отрезок А₁С₁, если АС = 18 см и АА₁:А₁В = 7:5.
7,5 см
Объяснение:
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Плоскость (АВС) проходит через прямую АС║α, значит плоскость (АВС) пересекает плоскость α по прямой, параллельной АС.
А₁С₁║АС.
Прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному, значит
ΔА₁ВС₁ ~ ΔАВС
По условию \dfrac{AA_{1}}{A_{1}B}=\dfrac{7}{5}
A
1
B
AA
1
=
5
7
то есть АА₁ составляет 7 частей, а А₁В - 5 частей, тогда АВ составляет 12 частей.
\dfrac{AC}{A_{1}C_{1}}=\dfrac{AB}{A_{1}B}=\dfrac{12}{5}
A
1
C
1
AC
=
A
1
B
AB
=
5
12
A_{1}C_{1}=\dfrac{5\cdot AC}{12}=\dfrac{5\cdot 18}{12}=\dfrac{15}{2}=7,5A
1
C
1
=
12
5⋅AC
=
12
5⋅18
=
2
15
=7,5 см
Пошаговое объяснение:
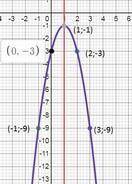
y = -2x² +4x -3
это парабола
коэффициент при х 2 > 0 - ветви вверх
модуль коэффициента > 1 - парабола сжата по отношению к графику у=х²
найдем дискриминант D
D=b² -4ac = -8
уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ
координаты вершины параболы
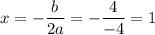
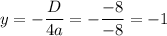
т.е. вершина параболы (1; -1)
ось симметрии
х = 1
координата у точки пересечения с осью оу (х=0)
у(0) = -2*0² +4*0 -3 = -3
т.е. точка пересечения с осью оу (0; -3)
симметричная ей точка относительно оси симметрии (2: -3)
для точности найдем еще пару точек
(-1; -9) и (3; -9)
наносим точки на координатную плоскость и строим график