144°
Пошаговое объяснение:
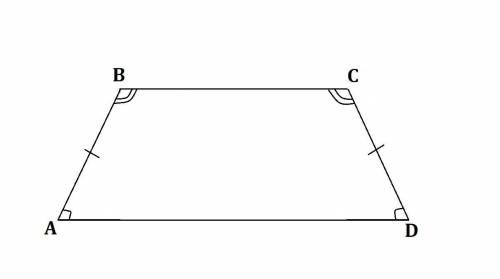
Обозначим данную трапецию буквами ABCD
По свойству равнобедренной трапеции ∠A = ∠D, ∠B = ∠C (также AB = CD)
По рисунку ∠B и ∠C - большие углы, ∠A и ∠D - меньшие углы.
****************
.1) Пусть x° - ∠A и ∠C, тогда 4x° - ∠B и ∠D.
Сумма внутренних углов любого четырёхугольника равна 360°.
4x + 4x + x + x = 360
10x = 360
x = 360: 10
x = 36
36° - меньший угол
Тогда 36° · 4 = 144° - больший угол
2) Можно было ещё по другому составить уравнение:
Пусть x° - ∠A, тогда 4x° - ∠B.
∠A и ∠B - внутренние односторонние при пересечении BC || AD секущей AB
⇒ ∠A + ∠B = 180°
x + 4x = 180
5x = 180
x = 180 : 5
x = 36
36° - меньший угол
Тогда 36° · 4 = 144° - больший угол.
.Так как ∠B > ∠A в 4 раза по условию, значит отношение большего угла к меньшему равно 4 : 1
4 + 1 = 5 (частей) - всего.
5 частей = 180°, так как ∠A + ∠B = 180° из 2)
180° : 5 = 36° - ∠A, то есть меньший угол
36° · 4 = 144° - ∠B, то есть больший угол
1. 9x*ctg113<= ctg473
ctg473=ctg(360+113)=ctg113 ( согласно формулам приведения). Этот угол (113 градусов) лежит во второй координатной четверти, где ctg альфа<= 0.
Имеем: 9x*ctg113<= ctg113. Разделим обе части неравенства на ctg113<0, при этом знак неравенства изменится на противоположный: 9x>=1, откуда х>=1/9 .
2. 3П/2меньше b меньше 2П - это 4-я четверть, где cosb>0, ctgb<0.
Согласно тождеству sin^2 x+cos^2 x=1, откуда cosх =+-корень(1- sin^2 x). Учитывая, что из-за 4-й четверти cosb>0, получим
cosb=корень(1- sin^2 b)=корень(1-(-5/13)^2)=корень(1-25/169)==корень(169/169-25/169)=корень(144/169)=12/13.ctgb=cosb/sinb=12/13 / (-5/13)=- 12/13*13/5=-12/5=-2,4
3) 5y+9y=14y
2) 7x-4x=3x
4) 6y-y=5y
5) x+4x+5x=10x
6) 8x+3x-x=10x
7) 10x+7x-8x= 9x
8) 9y+2y-4y=7y