Вариант 2
А1. Какая из пар чисел является решением линейного уравнения
321ху ?
1) 3;5
2) 3;5
3) 3;5
4) 3;5
А2. Для какого уравнения пара чисел 2;15
является решением?
1) 4567ху 2) 4567ху 3) 4567ху 4)
4567ху
А3. Решите систему уравнений
27,
341.
ху
ху
1) 3;0,5
2) 3;0,5
3) 3;2
4) 3;0,5
А4. Пусть
00;ху
- решение системы линейных уравнений
2316,
3422.
ху
ху
Найдите 00ху
. 1) 3
2) 3
3) 2
4) 1
А5. Пусть
00;ху
- решение системы линейных уравнений
213,
5433.
ху
ху
Найдите 00ху
. 1) 6
2) 8
3) 8
4) 7
А6. Пусть
00;ху
- решение системы линейных уравнений
44,
1632.
ху
ху
Найдите
0
0
х
у . 1)
0,5
2)
0,25
3)
0,4
4)
0,2
А7. На каком из рисунков изображено графическое решение системы линейных
уравнений
20,
24?
ху
ху
1) 2) 3) 4)
А8. Найдите координаты точки пересечения графиков уравнений 79ху
и 531ху .
1) 1;2
2) 1;2
3) 2;1
4) 1;1
А9. Сколько точек пересечения имеют графики уравнений 31ху и
623ух ?
1) 1 2) 2 3) бесчисленное количество 4) ни одной
А10. Сколько решений имеет система уравнений
25,
6315?
ху
ху
1) 1 2) 2 3) бесчисленное количество 4) ни одного
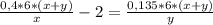
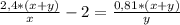
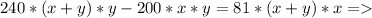
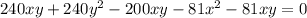
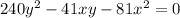
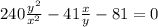
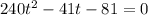
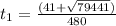
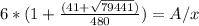
s(t)=t^3+3t^2
v(t)=3t^2+6t
v(1)=3+6=9 м/с
a(t)=6t+6
a(1)=6+6=12 м/с2
2.Найдите наибольшее значение функции y=-x^2-6x+5 на промежутке [-4,-2]
y=-x^2-6x+5
y`=-2x-6
y`=0 при х=-3 - принадлежит [-4,-2]
у(-4)=-(-4)^2-6*(-4)+5=13
у(-3)=-(-3)^2-6*(-3)+5=14
у(-2)=-(-2)^2-6*(-2)+5=13
наибольшее значение функции на промежутке [-4,-2]
max(y)=14
3.
y=корень(3) - горизонтальная прямая
касательная к прямой в любой точке совпадает с прямой
к оси абсцисс под углом 30 градусов касательная к прямой у=корень(3) быть не может
4.
y=(x-1)^3-3(x-1) =(x-1)((x-1)^2-3)=(x-1-корень(3))*(x-1)*(x-1+корень(3))
кривая третей степени,
симметричная относительно точки x=1; у=0
имеет локальный минимум и локальный максимум
имеет три нуля функции
имеет одну точку перегиба
расчетов не привожу так как это уже 4 задание в вопросе
график во вложении
3*. - для измененнного условия
y=корень(3x)
y`=1/2*корень(3/x)
y`=tg(pi/6)=корень(3)/3=1/2*корень(3/x)
корень(х)=3/2
х=2,25 - это ответ