Объяснение:
№1
А) (2х+1)²= 4х²+4х+1
Б) (3а-с)²= 9а²–6ас+с²
В) (а+6)(а-6)= а²–36
Г) (3х-4у) (3х+4у)= 9х²–16у²
№2
А) у²-¼= (у–½)(у+½)
Б) х²+10х+25= (х+5)²
№3
(2х-у)²-4х(х-у)= 4х²–4ху+у²–4х²+4ху= у²
при у= -⅔
(–⅔)²= 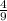
ответ: 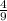
№4
А) 3(2а-b) (2a+b)= 3(4a²–b²)= 12a²–3b²
Б (х⁴+у³)² = (x^8)+2x⁴y³+(y^6)
В) (а+3b)²-(a-3b)²=(a+3b+a–3b)(a+3b–(a–3b))= a²(a+3b–a+3b)= a²*6b= 6a²b
№5
А) (2а-5)²-(2а-3) (2а+3)=0
(4a²–20a+25)–(4a²–9)=0
4a²–20a+25–4a²+9=0
–20a+34=0
20a=34
a= 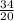
a= 1,7
Б) 9с²-25=0
(3c–5)(3c+5)=0
совокупность:
3с–5=0
3с+5=0
совокупность:
3с=5
3с=–5
совокупность:
с= 
с= 
совокупность:
с= 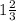
с= 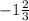
Пусть меньшая сторона — х метров, тогда большая — х+1 метров. Зная площадь площадки, составим и решим мат. модель:
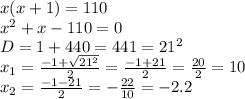
Отрицательный корень отбрасывает, т.к. длина не может быть отрицательной.
Следовательно, меньшая сторона — х = 10 метров;
большая — х+1 = 10+1 = 11 метров.
Для определения кол-ва упаковок материала для бордюра, вычислим периметр площадки:
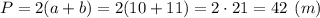
Необходимое количество упаковок равно:
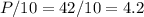
округляем с избытком до целого числа:
4.2 = 5
Меньшая сторона детской площадки равна: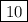 м.Большая сторона детской площадки равна:
м.Большая сторона детской площадки равна:  м.Необходимое количество упаковок равно:
м.Необходимое количество упаковок равно:  .
.
(x+7)(x-5)²=13(x-5)
(x+7)(x-5)²-13(x-5)=0
(х-5)((х+7)(х-5)-13)=0
(х-5)(х²-5х+7x-35-13)=0
(x-5)(x²+2x-48)=0
x-5=0
x=5
x²+2x-48=0
D=b²-4ac
D=2²-4×1×(-48)=4+192=√196=14
x1=-2-14/2 = -16/2 = -8
x2=-2+14/2 = 12/2 = 6
ответ: x=5, x1=-8, x2=6