6. -5 ≤ А ≤ 35
ответ 4).
7. 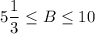
ответ 1)
Объяснение:
Требуется оценить выражение.
6.
-4 ≤ a ≤ 1; A = 3 - 8a
Если обе части неравенства умножить или разделить на отрицательное число, знак неравенства перевернется.Умножим все части неравенства на (-8), перевернув знаки неравенства:
-4 ≤ a ≤ 1 | · (-8)
32 ≥ -8a ≥ -8
или
-8 ≤ -8а ≤ 32
Если ко всем частям неравенства прибавить или отнять одно и то же число, то получим неравенство, равносильное данному.Прибавим ко всем частям неравенства 3:
3 - 8 ≤ 3 - 8а ≤ 3 + 32
-5 ≤ 3 - 8а ≤ 35
-5 ≤ А ≤ 35
ответ 4).
7.
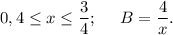
Переведем 0,4 в обыкновенную дробь.
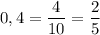
Перевернем наши дроби, при этом знак неравенства тоже перевернется:
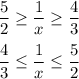
Умножим все части неравенства на 4:

ответ 1)
ДАНО
Y = x² - 6*x + 5 - уравнение параболы.
НАЙТИ
Ymin = ? - наименьшее значение.
РЕШЕНИЕ
Чтобы найти координаты вершины параболы преобразуем уравнение к виду
Y=(x - a)² +b
Y = (x² - 2*3x + 9) - 9 + 5 = (x-3)² - 4.
Вершина параболы: А(3;-4)
Ay = - 4 - наименьшее значение - ОТВЕТ
Точки пересечения с осями координат можно получить решением квадратного уравнения.
D = 16, x1 = 1, x2 = 5
Рисунок к задаче в приложении.
2. График параболы на рис. 2. Корни - х1 = - 1б х2 = 3, вершина А(1;4).
Но для решения задачи график не обязателен. Достаточно подставить значение У=3 и решить квадратное уравнение.
3 = - x² + 2*x + 3
- x² + 2*x = - x*(x-2) = 0
ОТВЕТ: х1 = 0, х2 = 2
Рисунок в приложении.
3. Каноническое уравнение параболы: Y= (x-a)² + b.
Координаты вершины такой параболы: Ах = - а, Ау = b.
Y = (x-3)² - уравнение параболы - дано.
Вершина с координатами: А(3;0), и ветви параболы - вверх.∫
Рисунок в приложении.