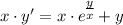
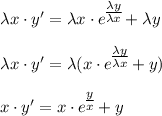
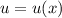 с замены:
с замены: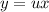 , тогда
, тогда 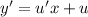
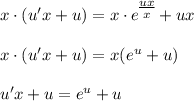
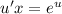
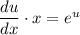 - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.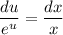 - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.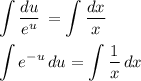
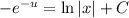 - общий интеграл новой функции.
- общий интеграл новой функции. из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену:
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: 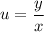
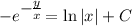 - общий интеграл исходного уравнения.
- общий интеграл исходного уравнения.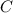 . Подставим в общий интеграл начальное условие:
. Подставим в общий интеграл начальное условие: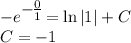
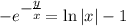 - частный интеграл, также является решением данного дифференциального уравнения.
- частный интеграл, также является решением данного дифференциального уравнения.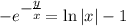
Убедимся, что данное дифференциальное уравнение является однородным.
То есть, воспользуемся условием однородности
Итак, данное дифференциальное уравнение является однородным.
Однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции
По определению дифференциала, получаем
Разделим переменные.
Проинтегрируем обе части уравнения
Таким образом, определив функцию
То есть,
Остаётся определить значение произвольной постоянной
ответ: