
Объяснение:
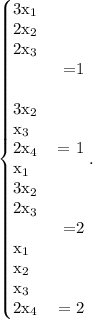
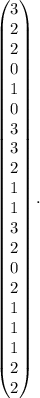
Поменяем местами 1-ю и 3-ю строки:

Вычитаем из 4-й строки 1-ю строку:

Вычитаем из 3-й строки 1-ю строку, умноженную на 3:

Разделим 2-ю строку на 3:

Суммируем 3-ю и 2-ю строку, умноженную на 7:

Суммируем 1-ю и 2-ю строку, умноженную на -3:

Суммируем 4-ю и 2-ю строку, умноженную на 2:

Поменяем местами 4-ю и 3-ю строки:

Суммируем 3-ю и 1-ю строки:

Суммируем 2-ю и 3-ю строку, умноженную на -1:

Суммируем 4-ю и 3-ю строку, умноженную на -3:

Разделим 4-ю строку на -16/3:

Суммируем 1-ю и 4-ю строку, умноженную на -4/3:

Суммируем 2-ю и 4-ю строку, умноженную на 8/3:

Суммируем 3-ю и 4-ю строку, умноженную на -10/3:


= 9sin^2 a + 9cos^2 a + 2sin^2 a + 6sin^4 a + 2(sin^4 a + 2cos^4 a) = (*)
Заметим, что
1) 9sin^2 a + 9cos^2 a = 9(sin^2 a + cos^2 a) = 9
2) sin^4 a + cos^4 a = sin^4 a + 2sin^2 a*cos^2 a + cos^4 a - 2sin^2 a*cos^2 a =
= (sin^2 a + cos^2 a)^2 - 2sin^2 a*cos^2 a = 1 - 1/2*(4sin^2 a*cos^2 a)
Подставляем
(*) = 9 + 2sin^2 a + 6sin^4 a + 2 - 4sin^2 a*cos^2 a =
= 11 + 4sin^2 a - 2sin^2 a + 6sin^4 a - 4sin^2 a*cos^2 a =
= 11 - 2sin^2 a + 6sin^4 a + 4sin^2 a*(1 - cos^2 a) =
= 11 - 2sin^2 a + 6sin^4 a + 4sin^4 a = 11 - 2sin^2 a + 10sin^4 a =
= 10(sin^4 a - 2*1/10*sin^2 a + 1/100) - 1/10 + 11 =
= 10(sin^2 a - 1/10)^2 + 109/10
Минимальное значение квадрата равно 0, а всего выражения 109/10.