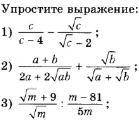
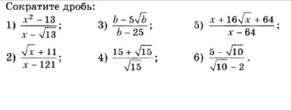
11 км
Объяснение:
Дано:
1) Скорость подъёма в гору v₁ = 3 км/час.
2) Скорость спуска с горы v₂ = 5 км/час.
3) Общее время подъёма в гору и спуска с горы 3 часа.
4) Известно также, что длина пути при подъёме в гору (s₁) на 1 км больше, чем длина пути при спуске с горы (s₂).
Найти: S - длину всего пройденного пути.
Решение.
1) Пусть х - время подъёма в гору, тогда (3-х) - время спуска с горы.
2) Длина пути при подъёме в гору:
s₁ = v₁ · t₁ = 3 · х
3) Длина пути при спуске с горы:
s₂ = v₂ · t₂ = 5 · (3-х)
4) Так как, согласно условию задачи, длина пути при подъёме в гору на 1 км больше, чем длина пути при спуске с горы, то можно составить уравнение и найти х:
s₁ - s₂ = 1
3 · х - 5 · (3-х) = 1
3х - 15 + 5х = 1
8 х = 1 + 15
8 х = 16
х = 2 часа - время подъёма в гору,
значит:
3 - х = 3 - 2 = 1 час - время спуска с горы.
5) Длина пути при подъёме в гору:
s₁ = v₁ · t₁ = 3 · 2 = 6 км
6) Длина пути при спуске с горы:
s₂ = v₂ · t₂ = 5 · 1 = 5 км
7) Длина всего пройденного пути:
S = s₁ + s₂ = 6 + 5 = 11 км
ответ: 11 км
Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
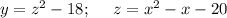
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
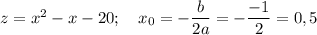 - координата вершины
- координата вершины
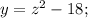 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
Извини за такой ответ. Тут я думаю можно использовать приложение Photomath. Я всегда им пользуюсь)