ответ : 4/15
метод подбора никто не отменял, поэтому рассуждаем, в числителе не может быть число меньше 4, так как по последнему условию если от числителя отнять 3, то дробь будет положительной.
Предположим, что числитель 4, тогда знаменатель должен быть равен
4²-1( по условию: знаменатель меньше квадрата числителя на единицу) =15.
Полученную дробь проверяем на остальные условия:
1условие: (4+2)/(15+2)>1/3;
6/15>1/3 ;
6/15>1*5/3*5
6/15>5/15 - верно
2 условие
0<(4-3)/(15-3)<1/10
0<1/12<1/10- верно
ответ: 4/15
Уравнение:
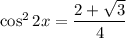
Предлагаю применить формулу косинуса половинного угла (она выглядит вот так: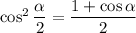 
):
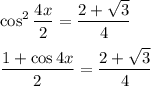
Теперь домножим обе части уравнения на четыре (чтобы "избавиться от дробей") + упростим получившееся выражение:
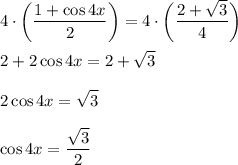
Мы получили выражение вида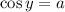 
(в нашем случае 
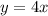). Оно решается по формуле: 
, 
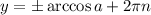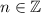. Значит:
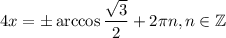
А также вспомним, что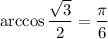 
:
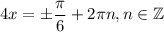
И, на всякие случай, поделим все на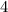 
:
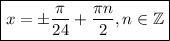
Теперь найдем наименьшее положительное решение уравнения. Понятно, что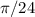 
нужно взять с "плюсом" (чтобы и в итоге получился "плюс"), а также 
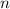приравнять нолю:
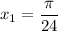
Получился как раз последний вариант ответа!
ответ: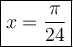 
Б) 2y+x-2xy-x²
В) 25c²-40c+16